BLOG DE ALFABETIZACIÓN MATEMÁTICA “DORA - SHEIKHA MAHRA BINT MOHAMMED BIN RASHID AL MAKTOUM”. Educación científica trilingüe.
"DORA - SHEIKHA MAHRA BINT MOHAMMED BIN RASHID AL MAKTOUM" MATHEMATICAL LITERACY BLOG. Trilingual science education.
"DORA - SHEIKHA MAHRA BINT MOHAMMED BIN RASHID AL MAKTOUM" BLOG DE LITTÉRATIE MATHÉMATIQUE. Enseignement trilingue des sciences.
PAGE 3
CAPÍTULO IV: "LEYES DE NEWTON: EXPLICANDO EL MOVIMIENTO"
CHAPTER IV: "NEWTON'S LAWS: EXPLAINING MOTION"
CHAPITRE IV : "LES LOIS DE NEWTON : EXPLIQUER LE MOUVEMENT"
Los experimentos de Galileo lo llevaron a atribuir a todos los cuerpos una propiedad denominada inercia.
Osorno (1992) propuso para la inercia la siguiente definición:
Es la imposibilidad de cambiar el estado de reposo o de movimiento uniforme de los cuerpos sin interactuar con ellos (y esa imposibilidad no se mide).
El enunciado formal del Principio de inercia es el siguiente: Todo cuerpo sobre el cual no actúan fuerzas, se mantiene en su estado de reposo o de movimiento uniforme en línea recta.
Varios hechos ligados a la experiencia diaria se relacionan con el concepto de inercia. Las figuras M-34, M-35, M-36, M-37 y M-38 ilustran casos en donde la inercia desempeña un papel importante. Se hará un análisis detallado de cada uno de esos casos en el capítulo V.
-----------------------------------------------------------------------------------------------------
FRANK: "Te sugiero que estudies los capítulos IV y V como si conformaran un sólo bloque."
ORYX: "De acuerdo."
------------------------------------------------------------------------------------------------------
En el ascensor (ver figura M-34)
En el autobús (ver figura M-35)
En la carretera (ver figura M-36)
Un niño que se columpia (ver figura M-37 y M-38)
Estas situaciones de nuestra vida cotidiana y su vinculación con la ley de la inercia serán explicadas de manera detallada en el capítulo V.






FRANK: "Te sugiero que repases el capítulo II, antes de iniciar la lectura de esta parte del capítulo IV."
ORYX: "De acuerdo."
-----------------------------------------------------------------------------------------------------
En Física decimos que un cuerpo está en movimiento con respecto a otro cuando su posición respecto a ese cuerpo está cambiando al transcurrir el tiempo. Por ejemplo, se dice que el chofer que conduce una camioneta se encuentra en movimiento con respecto a un árbol cuando, al transcurrir el tiempo, la posición del chofer con respecto a ese árbol va cambiando (ver figura M-39).
Por otra parte, si la posición de un cuerpo con respecto a otro no cambia al transcurrir el tiempo decimos que ese cuerpo se encuentra en reposo. El chofer de la camioneta se encuentra en reposo. El chofer de la camioneta se encuentra en reposo con respecto al pasajero que va en el asiento trasero si al transcurrir el tiempo su posición no cambia con respecto a aquel.
El reposo y el movimiento son conceptos relativos; esto es, dependen del cuerpo que se emplee como referencia. En nuestro caso, el chofer está en reposo con respecto al pasajero, pero en movimiento con respecto al poste. Para describir el movimiento de un cuerpo es necesario seleccionar un sistema de referencia. Un sistema de referencia es cualquier cuerpo o punto que se selecciona para describir la posición o el movimiento de otros cuerpos. Es conveniente señalar que la elección de nuestro sistema de referencia puede complicar o simplificar la descripción del movimiento del cuerpo que se estudia. Por ello, es recomendable elegir aquel sistema de referencia que nos facilite la descripción del movimiento; así, para describir el movimiento de la Luna se selecciona a la Tierra y no a otros planetas (ver figura M-40).
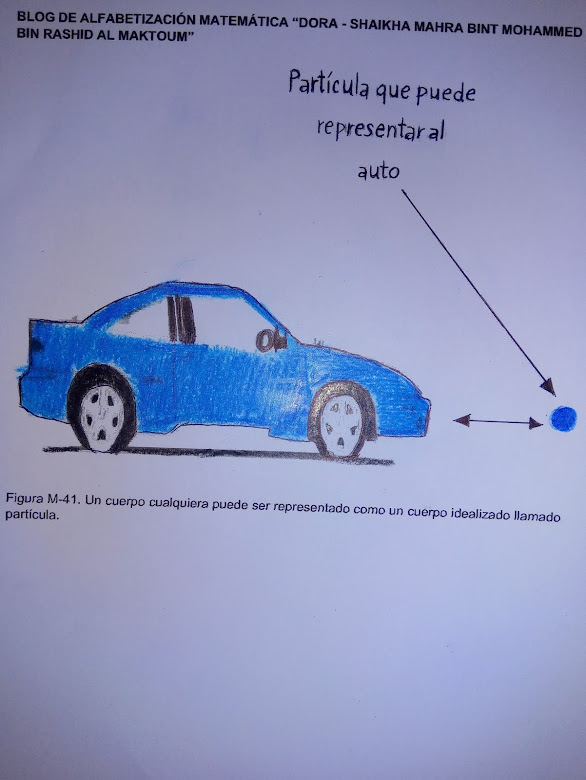
Una partícula es un cuerpo de dimensiones muy pequeñas que tiene masa. En los esquemas, puede representarse por un punto. Un cuerpo cualquiera puede ser representado como un cuerpo idealizado llamado partícula (ver figura M-41).
Dinámica: Parte de la Física encargada de estudiar el movimiento de un cuerpo analizando los factores que lo originan.
Problema fundamental de la dinámica: Conocidas las causas que determinan el movimiento, encontrar el vector de posición y la velocidad.
Aproximación de punto material o partícula: Todo cuerpo que es considerado como un punto geométrico al que se le asocia una cierta masa.
Medio: Dada una partícula, se define su medio como el resto de partículas del Universo. Influencia que ejerce el medio sobre la partícula.
Partícula libre: Aquélla que no está sujeta a ningún tipo de interacción con el medio.

-----------------------------------------------------------------------------------------------
*Si no tiene tiempo de leerlos ahora, descárguelos, imprímalos y hágalo cuando le interese (archivos en formato PDF).
If you don't have time to read them now, download, print off and take away with you (archives in PDF format).
------------------------------------------------------------------------------------------------------
https://drive.google.com/file/d/1ww91c3FCl-Gb5rSMTL5iqywwW-6erK6C/view?usp=sharing


FRANK: “Vamos a aprender una ampliación de algo que hemos aprendido anteriormente.”
ORYX: “De acuerdo”
--------------------------------------------------------------------------------------------------------------------
+¿En qué condiciones debe tratarse como una partícula a un cuerpo? Un cuerpo puede ser representado como una partícula cuando:
1. Sus dimensiones sean muy pequeñas en comparación con la distancia recorrida. El movimiento de la Tierra alrededor del Sol puede considerarse como el movimiento de una partícula (figura M-40).
2. Su movimiento sea de traslación, es decir, cuando cada segmento del cuerpo se mantenga paralelo a sí mismo durante su movimiento (figura M-42).

--------------------------------------------------------------------------------------------------------------------
ACTIVIDADES CON EL PENTASOFTWARE:
FRANK: "Vamos a continuar aprendiendo sobre vectores y Leyes de Newton pero haciendo uso del Pentasoftware, el cual consta de 5 softwares educativos. Vamos a emplear el Pentasoftware en la versión de fotogramas."
ORYX: "Excelente. Pero, ¿qué es un fotograma?"
FRANK: "Según la Real Academia de la Lengua Española es cada una de las imágenes que se suceden en una película cinematográfica."
ORYX: "¿Acaso vamos a ver películas?"
FRANK: "No. Vamos a captar fotogramas usando como herramienta tecnológica el celular Motorola Moto G7 Power. Tal como lo describe la empresa Motorola, la cámara cuenta con software inteligente y ofrece diferentes opciones, como el retrato o la posibilidad de crear cinemagrafías manteniendo una parte de la toma en movimiento mientras se congela todo lo demás."
ORYX: "¿Y qué vamos a fotografiar?"
FRANK: "Vamos a fotografiar la pantalla de una computadora de escritorio. Específicamente, una computadora HP-All-in-One-20-c414la (Hewlett Packard Company). Se van a fotografiar las imágenes provenientes de 5 softwares (los cuales iremos conociendo de manera paulatina). Así vamos a lograr un aprendizaje significativo de los vectores y las Leyes de Newton. Pero hay algo que también es de suma importancia."
ORYX: "¿A qué se refiere con eso?"
FRANK: "Es algo que por ahora me voy a limitar a decirte su "nombre científico": REGISTROS DE REPRESENTACIONES SEMIÓTICAS. Esto es muy útil en tu proceso de aprendizaje de Ciencias Físicas y Matemáticas. En los siguientes capítulos veremos de manera práctica y paulatina varias cosas referentes a los registros de representaciones semióticas, las imágenes estroboscópicas y los fotogramas provenientes del Pentasoftware."
ORYX: "Eso es muy interesante."
-------------------------------------------------------------------------------------------------------
*Chams-eddine Khiari (2011) expresó lo siguiente:
El Principio de inercia: Muy a menudo se le llama "la primera ley del movimiento" como si las palabras principio y ley fueran sinónimos.
Es bien sabido que este "principio" no tiene ninguna prueba experimental directa. Es sólo una generalización (una extrapolación "idealizada").
De hecho, el mencionado "principio" es sólo una hipótesis; este último se define como una proposición resultante de una observación y que se somete al control del experimento, o que se verifica por deducción. No es un axioma, como sugieren algunos autores, si un axioma se define como una verdad indemostrable que se impone con la fuerza. Tampoco es una ley; este último se define como una proposición general que establece relaciones necesarias y constantes entre fenómenos físicos o entre los constituyentes de un conjunto. Este término debería reservarse a interacciones fundamentales como, por ejemplo, la interacción gravitacional universal. En todos los casos, está lejos de constituir un principio universal porque no hay experiencia que lo pruebe o refute.
Es cierto que el concepto de inercia está lejos de lograrse teóricamente como sugieren muchos libros y artículos publicados.
Por último, se señala que el "principio de inercia" necesita el "tercer principio" para ser justificado.
Chams-eddine Khiari (2011) said the following:
The inertia Principle: It is very often called “the first law of motion” as if the words principle and law were synonymous.
It is well known that this “principle” does not have any direct experimental proof. It is only a generalization (an “idealized” extrapolation).
In fact, the aforementioned “principle” is only a hypothesis; the latter being defined as a proposition resulting from an observation and that one subjects to the control of experiment, or that one verifies by deduction. It is not an axiom, as some authors suggest, if an axiom is defined as an indemonstrable truth which imposes itself with force. It is not a law either; the latter being defined as a general proposition stating necessary and constant relationships between physical phenomena or between the constituents of an ensemble. This term should be reserved to fundamental interactions such as, for example, the universal gravitational interaction. In all cases, it is far from constituting a universal principle because there is no experience to prove or refute it.
It is certain that the concept of inertia is far from being theoretically achieved as many published books and articles suggest.
One finally notes that the “principle of inertia” needs the “third principle” to be justified.
-----------------------------------------------------------------------------------------------------------------
ORYX: “¿ Entonces lo que aprendimos en capítulos anteriores sobre el “Principio” de Inercia es incorrecto?”
FRANK: “Ya hemos aprendido que no es apropiado el término “principio”, pues existen fundamentos para emplear el término hipótesis. Pero lo que aprendimos en capítulos anteriores es “aceptado” en la mayoría de los libros de texto de Educación Secundaria y Bachillerato. Pero es bueno que aprendas lo importante que es realizar críticas incluso a los libros de texto, a cualquiera que llegue a tus manos, ya sea de forma de papel o de forma virtual. Saber discernir y seleccionar información científica de libros de texto, revistas científicas, tesis universitarias, seminarios, congresos, etc. es algo que se aprende con la experiencia con el paso de los años de estudio. De manera implícita, uno de los objetivos del presente blog es apoyarte en ese aspecto del aprendizaje.
ORYX: “Esto es muy interesante. ¿ Qué vamos a aprender a continuación?"
FRANK: “Modelación matemática de las Leyes de Newton y registros de representaciones semióticas asociados a vectores."
ORYX: "Muy interesante."
------------------------------------------------------------------------------------------------------------------
Se sugiere usar BING TRANSLATOR para fortalecer la habilidad de escucha en el aprendizaje de idiomas extranjeros.
It is suggested to use BING TRANSLATOR to strengthen listening skills in foreign language learning.
-----------------------------------------------------------------------------------------------------------------
*Un punto de vista matemático es considerar esta ciencia como un estudio de modelos.
One way to view mathematics is to think of it as a study of patterns.
*En términos generales, una ecuación o una función que se construye con base en ciertos supuestos sobre alguna situación o fenómeno del mundo real con la intención de describir dicho fenómeno se denomina modelo matemático.
In rough terms , an equation or a function that is constructed using certain assumptions about some real-world situation or phenomenon with the intent to describe that phenomenon is said to be a mathematical model.
*Hablando con generalidad, un modelo matemático es una descripción matemática de algo que se llama sistema . Para construir un modelo matemático se comienza con un conjunto de hipótesis razonables acerca del sistema que se esté tratando de describir. En estas hipótesis se incluyen todas las leyes empíricas que sean aplicables al sistema. El resultado final podría ser una descripción tan simple como lo es una función.
Roughly speaking , a mathematical model is a mathematical description of something that we will call a system. To construct a mathematical model we start with a set of reasonable assumptions about the system that we are trying to describe. These assumptions include any empirical laws that are applicable to the system. The end result could be a description as simple as a single function.
*Los problemas reales son a veces tan complicados que una solución exacta es imposible o requiere medidas o cálculos extremadamente difíciles. Una estimación aproximada de la solución correcta puede hallarse a menudo con un modelo matemático obtenido a partir de hipótesis simplificadoras y de aproximaciones.
Real problems sometimes are so complex that an exact solution is either impossible or else requires very difficult measurements or calculations. A rough estimate of the correct solution can often be found with a mathematical model obtained by making simplifying assumptions and approximations.
*Los modelos matemáticos pueden mostrar cuáles son los factores importantes de un problema y facilitar una comprensión cualitativa que no se podría obtener a partir de una aproximación más exacta. Sus predicciones pueden indicar si vale la pena un esfuerzo más elaborado y pueden sugerir líneas de ataque para tales esfuerzos.
Mathematical models can show what factors are important in a problem and provide a qualitative understanding that may not be obtainable from a more exact approach. Their predictions may indicate whether a more elaborate effort is worth attempting and may suggest lines of attack for such an effort.
*La importancia del álgebra lineal para las aplicaciones se ha elevado en proporción directa al incremento en la potencia de cómputo. Con cada nueva generación de hardware y software se dispara una demanda de mayor capacidad. La ciencia de cómputo está así intrincadamente ligada al álgebra lineal, a través del crecimiento explosivo del procesamiento en paralelo y de los cálculos en gran escala. Hoy,el álgebra lineal tiene más valor potencial para los estudiantes en muchos campos científicos y de negocios que cualquier otra materia de matemáticas de licenciatura.
The importance of linear algebra for applications has risen in direct proportion to the increase in computing power, with each new generation of hardware and software triggering a demand for even greater capabilities. Computer science is thus intricately linked with linear algebra through the explosive growth of parallel processing and large-scale computations. Today, linear algebra has more potential value for students in many scientific and business fields than any other undergraduate mathematics subject.
*En el presente blog proporcionamos los principios del álgebra lineal.
In this blog we provide the principles of linear algebra.
*La mayoría de docentes de ciencias reconocen explícitamente la importancia de resaltar el vínculo entre el Álgebra Lineal y la Geometría Analítica (Kozak,Pastorelli, Vardanega, 2007; Heinhold , Riedmuller, 1980).
Most science teachers explicitly recognize the importance of highlighting the link between Linear Algebra and Analytic Geometry (Kozak,Pastorelli, Vardanega, 2007; Heinhold , Riedmuller, 1980).
+ La noción de predicción resulta ser una de las características esenciales de las teorías físicas (Holton, 1979, pp. 51-53). Con esto concordaron Helfgott, Vera (1989), matemáticos peruanos, quienes manifestaron que todos los científicos aceptan un modelo en la medida que las consecuencias que de él se deriven no contradigan a los datos experimentales. Se cumple un ciclo triangular. Estos notables matemáticos también expresaron que muchas veces la naturaleza guarda sus secretos en forma de ecuaciones diferenciales; es tarea del científico develar esos misterios y obtener consecuencias de las ecuaciones para ser contrastadas con la realidad, que en último término es el supremo árbitro en la determinación de la validez de un modelo. Existe una diferencia entre verdad matemática y verdad científica. Respecto a la verdad matemática, tenemos que es fácil de definir y comprobar; sólo se aceptan proposiciones que se deducen estrictamente de los axiomas, teoremas, proposiciones anteriores, etc. En cuanto a la verdad científica, ésta es mucho más difícil de definir. Este aspecto está íntimamente ligado al rol que juegan los modelos matemáticos en las ciencias experimentales. Los modelos matemáticos son útiles no sólo porque sistematizan y explican datos conocidos en base a leyes generales, sino porque predicen fenómenos.

Ciclo triangular de un modelo científico (Helfgott, Vera, 1989, p. 58)
----------------------------------------------------------------------------------------------------

PRIMERA LEY DEL MOVIMIENTO DE NEWTON EN NUESTRA VIDA COTIDIANA

+Para elaborar un enfoque alternativo de las leyes de Newton consideramos las ideas de Arribas; Sanjosé (1992) ; Hewitt (2007). Este último investigador manifestó que la cantidad de movimiento es una extensión lógica de la tercera ley de Newton.
+La mecánica de Newton se construye a partir del concepto de inercia. Una vez establecida la inercia como la ley fundamental del movimiento, se introduce la definición de fuerza a partir de la cual es posible definir procedimientos de medición de las magnitudes físicas involucradas en la mecánica. Aparece el concepto de conservación de la cantidad de movimiento y se definen los criterios para establecer cuándo un sistema físico se puede considerar aislado. El concepto de masa adquiere pleno significado físico como medida de la inercia de los cuerpos a partir del concepto de fuerza y de la tercera ley de Newton. Usando el concepto de la cantidad de movimiento, se parte del principio de su conservación (análogo a la primera ley del movimiento de Newton). Luego de que se define el concepto de fuerza, la segunda ley del movimiento de Newton surge como un teorema, y la tercera como un corolario.
+Cuando lanzamos un cuerpo sobre una mesa, el cuerpo se para después de una distancia. Si pulimos la mesa y el cuerpo, el cuerpo irá más lejos. Si ponemos un colchón de aire debajo del cuerpo, eliminamos prácticamente cualquier rozamiento, el cuerpo continúa su camino sin pararse aparentemente y la medida de su velocidad nos indica que es casi constante.
En el espacio, los satélites artificiales , cuando están lejos de cualquier cuerpo celeste, se desplazan rigurosamente en línea recta y a velocidad constante sin consumir combustible.
+De estos hechos experimentales, podemos deducir que:
Todo cuerpo continúa en su estado de reposo o de movimiento rectilíneo uniforme , si no recibe ninguna intervención del exterior.
+En otras palabras, el movimiento de un cuerpo sobre el cual no actúan fuerzas, no es acelerado.
Expresado de otras maneras:
"Si no actúan fuerzas sobre un cuerpo éste continuará moviéndose con velocidad uniforme o se mantendrá en reposo."
Equivalente a decir que : "Un cuerpo no cambia su estado de movimiento en forma espontánea." o "Todo cuerpo tiene inercia."
+Esa ley, conocida también como principio de inercia describe el comportamiento natural de los cuerpos en ausencia de interacción, estableciendo tanto el reposo como el movimiento uniforme como dos estados equivalentes. Es realmente difícil (si no imposible) liberar a un cuerpo de toda interacción, lo cual no permite una comprobación experimental de esta ley.
*Una particula libre es aquella que no está sujeta a interacción alguna. Estrictamente no existe tal cosa, ya que toda partícula está sujeta a interacciones con el resto del mundo. Luego, una partícula libre deberá estar completamente aislada, o ser la única partícula en el mundo. Pero entonces sería imposible obervarla porque, en el proceso de la observación, hay siempre una interacción entre el observador y la partícula. En la práctica, sin embargo, hay algunas partículas que podemos considerar libres, ya sea porque se encuentran suficientemente lejos de otras y sus interacciones son despreciables, o porque las interacciones con las otras partículas se cancelan, dando una interacción total nula.
A free particle is one that is not subject to any interaction. Strictly speaking, there is no such thing, because each particle is subject to interactions with the rest of the particles in the world. Therefore, a free particle should either be completely isolated, or else be the only particle in the world. But then it would be impossible to observe it because, in the process of observation, there is always an interaction between the observer and the particle. In practice, however, there are some particles which may be considered free, either because they are sufficiently far away from others for their interactions to be negligible, or because the interactions with the other particles cancel, giving a zero net interaction.
+ Se supone que existen partículas libres, definidas como aquéllas cuya interacción total con el resto del Universo puede ser despreciada.
*En otras palabras, consideremos ahora la ley de la inercia la cual establece que: "Una partícula libre se mueve siempre con velocidad constante, o (lo que es lo mismo) sin aceleración."
In other words, let us now consider that the law of inertia, which states that: " A free particle always moves with constant velocity or (which amounts to the same thing) without acceleration."
Esto es, una partícula libre se mueve en línea recta con una velocidad constante o se encuentra en reposo (velocidad cero). Esta proposición se denomina la Primera Ley del movimiento de Newton, porque fue inicialmente propuesta por Sir Isaac Newton (1642-1727).

+Es la ley de la inercia o Primera Ley del movimiento de Newton. Esta ley implica que:
*Ninguna explicación es necesaria para justificar la existencia de una velocidad.
*Para cambiar la dirección o la magnitud de la velocidad de un cuerpo, es decir, para producir una aceleración, se necesita una interacción del exterior del cuerpo.
Respecto a la figura M-29-c y lo expresado por Galileo, podemos afirmar que fue Newton quien se dio cuenta de que hay más que decir que esto. A menos que algo del exterior aplique una fuerza para cambiarlo, la velocidad de un objeto (tanto su velocidad como su dirección) debe seguir siendo la misma.
+Hay dos informaciones contenidas en la ley de la inercia:
*La primera es la definición cualitativa de fuerza. La fuerza es la causa del movimiento y su presencia es necesaria para alterar el estado de movimiento del cuerpo. La fuerza es un agente de cambio, no la causa del movimiento.
*La segunda información es la de que el reposo ( vector velocidad es igual a cero) y el movimiento rectilíneo uniforme (vector velocidad es igual a una constante) son dos estados enteramente equivalentes para los puntos materiales. Los conceptos de reposo y de movimiento uniforme son relativos y equivalentes; para alterar cualquiera de ellos es preciso aplicar una fuerza (Hech, 1987). Estas fuerzas impresas son las que permiten cambiar el estado de reposo o de movimiento uniforme de un cuerpo.
+Si observas atentamente el movimiento de un cuerpo , como el de una pelota de béisbol, verás que ésta gira sobre su propio eje mientras se desplaza. De igual manera, al observar el movimiento de la caída de una hoja que fue arrancada de un árbol por el viento, veremos que la hoja gira y se enrosca mientras se desliza hacia la izquierda y hacia la derecha, como flotando, durante su descenso. La descripción de este tipo de movimiento es muy complicado. Un cuerpo también puede vibrar durante su movimiento (como es el caso del motor de un automóvil sin afinar). Esto hace evidente la variedad y complejidad del movimiento de los cuerpos. Las complicaciones pueden evitarse si se considera a los cuerpos como partículas.
+El punto material no es un cuerpo geométrico , pues posee una propiedad que los puntos geométricos no tienen, que es la masa inercial ; esta propiedad está íntimamente ligada al movimiento de los cuerpos , como podemos ver cuando tratamos de entender cómo se mueven los cuerpos.
+Ningún cuerpo se opone o se resiste al movimiento, ni tiende al reposo como se afirma frecuentemente. Para que un cuerpo deje el reposo la fuerza neta que actúe sobre él debe ser distinta de cero. Sobre un objeto que se mueve con velocidad constante también hay que interactuar si se lo quiere detener ; si existe rozamiento, esta fuerza terminará deteniéndolo ; si no, debemos interactuar con él de alguna manera para que se detenga. La fuerza es un agente de cambio , no la causa del movimiento.
Cuando se trata de explicar lo que sucede dentro de un bus que frena o acelera , se recurre a la ley de la inercia , diciendo que un objeto colocado sobre el piso se desplaza hacia adelante o hacia atrás , porque por inercia tiende a conservar el movimiento que llevaba , olvidando que el bus en esas condiciones no se puede considerar como un sistema de referencia inercial.
Se debe recordar que con la primera ley se postula la existencia de los sistemas inerciales de referencia , sistemas ligados a una partícula libre y únicos sistemas donde son válidas las leyes de Newton , por lo tanto la ley de la inercia no se cumple en los sistemas acelerados.
Un sistema de referencia ligado a una partícula libre es llamado sistema de referencia inercial , SRI. Cualquier otro sistema se denomina sistema de referencia no inercial , SRNI.
+Suponga que está en un autobús que viaja por una carretera recta y acelera. Si pudiera pararse en el pasillo usando patines, comenzaría a moverse hacia atrás relativo al autobús, conforme éste aumenta de rapidez. En cambio , si el autobús frenara , usted comenzaría a moverse hacia delante, respecto del autobús , por el pasillo. En ambos casos , parecería que no se cumple la primera Ley de Newton : no actúa una fuerza neta sobre usted , pero su velocidad cambia. ¿Qué sucede aquí?
La cuestión es que el autobús acelera con respecto al suelo y no es un marco de referencia adecuado para la primera ley de Newton. Ésta es válida en algunos marcos de referencia , pero no en otros. Un marco de referencia en el que es válida la primera ley de Newton es un marco de referencia inercial. La Tierra es aproximadamente un marco de referencia inercial , pero el autobús no ( la Tierra no es un marco plenamente inercial debido a la aceleración asociada a su rotación y a su movimiento alrededor del Sol , aunque tales efectos son pequeños ; ver la figura M-44). Como usamos la primera ley de Newton para definir lo que es un marco de referencia inercial , se le conoce como ley de inercia.
*Un sistema situado en la Tierra no es inercial debido a la rotación diaria de la tierra y a su movimiento acelerado alrededor del sol. El sol igualmente no es un sistema inercial debido a su movimiento alrededor del centro de la galaxia. Sin embargo, para propósitos prácticos cualquiera de estos cuerpos puede utilizarse para definir un sistema inercial.
A coordinate system attached to the earth is not inertial because of its daily rotation and its accelerated motion around the sun. Nor is the sun an inertial frame because of its motion about the center of the galaxy. However, for practical purposes, either of these two bodies may be used to define an inertial frame.
+¿Cómo se puede estar seguro de que un marco de referencia es inercial o no lo es? Verificando si es válida la primera ley de Newton. De esta forma , la primera ley de Newton sirve como definición de los marcos de referencia inerciales.
+El espacio y el tiempo son conceptos fundamentales de la Mecánica : a cada tiempo , la posición de una partícula está determinada por una terna de números reales que son su vector posición r (t) = (x,y,z).
La forma más simple de definir estos números es mediante coordenadas cartesianas con respecto a un origen y unos ejes ortogonales , que constituyen un sistema de referencia.
Dado un sistema de referencia , las coordenadas cartesianas no son las únicas posibles para determinar los tres parámetros espaciales de la posición de una partícula. Se pueden usar coordenadas polares (en el plano ), esféricas, cilíndricas, ...las que convenga.
+En Dinámica existen dos tipos de sistemas de referencia : los sistemas inerciales y los no inerciales.
a) Sistemas inerciales: Un sistema es inercial cuando está en reposo o tiene movimiento rectilíneo y uniforme. Para un sistema inercial son válidas las leyes de Newton. En un sistema inercial solamente producen aceleración las fuerzas reales.
b)Sistemas no inerciales: Un sistema no inercial es aquel que tiene aceleración. Para que se cumplan las Leyes de Newton en estos sistemas hay dos soluciones:
1.- Suponer que los efectos de la aceleración del sistema son despreciables, cosa imposible en muchos casos.
2.- Introducir unas fuerzas ficticias o inerciales causantes de esa aceleración.
En un sistema de referencia inercial se cumple la primera ley de Newton. Por ejemplo, un tren que se mueve en línea recta a velocidad constante es un sistema de referencia inercial , ya que en él , un cuerpo en reposo permanecerá en reposo , y una canica que se deslice sobre un vidrio sin fricción , se moverá en línea recta a velocidad constante con respecto al tren , independientemente de la velocidad del tren. Ver figura M-45.

+Es la ley de la inercia o Primera Ley del movimiento de Newton. Esta ley implica que:
*Ninguna explicación es necesaria para justificar la existencia de una velocidad.
*Para cambiar la dirección o la magnitud de la velocidad de un cuerpo, es decir, para producir una aceleración, se necesita una interacción del exterior del cuerpo.
Respecto a la figura M-29-c y lo expresado por Galileo, podemos afirmar que fue Newton quien se dio cuenta de que hay más que decir que esto. A menos que algo del exterior aplique una fuerza para cambiarlo, la velocidad de un objeto (tanto su velocidad como su dirección) debe seguir siendo la misma.
+Hay dos informaciones contenidas en la ley de la inercia:
*La primera es la definición cualitativa de fuerza. La fuerza es la causa del movimiento y su presencia es necesaria para alterar el estado de movimiento del cuerpo. La fuerza es un agente de cambio, no la causa del movimiento.
*La segunda información es la de que el reposo ( vector velocidad es igual a cero) y el movimiento rectilíneo uniforme (vector velocidad es igual a una constante) son dos estados enteramente equivalentes para los puntos materiales. Los conceptos de reposo y de movimiento uniforme son relativos y equivalentes; para alterar cualquiera de ellos es preciso aplicar una fuerza (Hech, 1987). Estas fuerzas impresas son las que permiten cambiar el estado de reposo o de movimiento uniforme de un cuerpo.
+Si observas atentamente el movimiento de un cuerpo , como el de una pelota de béisbol, verás que ésta gira sobre su propio eje mientras se desplaza. De igual manera, al observar el movimiento de la caída de una hoja que fue arrancada de un árbol por el viento, veremos que la hoja gira y se enrosca mientras se desliza hacia la izquierda y hacia la derecha, como flotando, durante su descenso. La descripción de este tipo de movimiento es muy complicado. Un cuerpo también puede vibrar durante su movimiento (como es el caso del motor de un automóvil sin afinar). Esto hace evidente la variedad y complejidad del movimiento de los cuerpos. Las complicaciones pueden evitarse si se considera a los cuerpos como partículas.
+El punto material no es un cuerpo geométrico , pues posee una propiedad que los puntos geométricos no tienen, que es la masa inercial ; esta propiedad está íntimamente ligada al movimiento de los cuerpos , como podemos ver cuando tratamos de entender cómo se mueven los cuerpos.
+Ningún cuerpo se opone o se resiste al movimiento, ni tiende al reposo como se afirma frecuentemente. Para que un cuerpo deje el reposo la fuerza neta que actúe sobre él debe ser distinta de cero. Sobre un objeto que se mueve con velocidad constante también hay que interactuar si se lo quiere detener ; si existe rozamiento, esta fuerza terminará deteniéndolo ; si no, debemos interactuar con él de alguna manera para que se detenga. La fuerza es un agente de cambio , no la causa del movimiento.
Cuando se trata de explicar lo que sucede dentro de un bus que frena o acelera , se recurre a la ley de la inercia , diciendo que un objeto colocado sobre el piso se desplaza hacia adelante o hacia atrás , porque por inercia tiende a conservar el movimiento que llevaba , olvidando que el bus en esas condiciones no se puede considerar como un sistema de referencia inercial.
Se debe recordar que con la primera ley se postula la existencia de los sistemas inerciales de referencia , sistemas ligados a una partícula libre y únicos sistemas donde son válidas las leyes de Newton , por lo tanto la ley de la inercia no se cumple en los sistemas acelerados.
Un sistema de referencia ligado a una partícula libre es llamado sistema de referencia inercial , SRI. Cualquier otro sistema se denomina sistema de referencia no inercial , SRNI.
+Suponga que está en un autobús que viaja por una carretera recta y acelera. Si pudiera pararse en el pasillo usando patines, comenzaría a moverse hacia atrás relativo al autobús, conforme éste aumenta de rapidez. En cambio , si el autobús frenara , usted comenzaría a moverse hacia delante, respecto del autobús , por el pasillo. En ambos casos , parecería que no se cumple la primera Ley de Newton : no actúa una fuerza neta sobre usted , pero su velocidad cambia. ¿Qué sucede aquí?
La cuestión es que el autobús acelera con respecto al suelo y no es un marco de referencia adecuado para la primera ley de Newton. Ésta es válida en algunos marcos de referencia , pero no en otros. Un marco de referencia en el que es válida la primera ley de Newton es un marco de referencia inercial. La Tierra es aproximadamente un marco de referencia inercial , pero el autobús no ( la Tierra no es un marco plenamente inercial debido a la aceleración asociada a su rotación y a su movimiento alrededor del Sol , aunque tales efectos son pequeños ; ver la figura M-44). Como usamos la primera ley de Newton para definir lo que es un marco de referencia inercial , se le conoce como ley de inercia.
*Un sistema situado en la Tierra no es inercial debido a la rotación diaria de la tierra y a su movimiento acelerado alrededor del sol. El sol igualmente no es un sistema inercial debido a su movimiento alrededor del centro de la galaxia. Sin embargo, para propósitos prácticos cualquiera de estos cuerpos puede utilizarse para definir un sistema inercial.
A coordinate system attached to the earth is not inertial because of its daily rotation and its accelerated motion around the sun. Nor is the sun an inertial frame because of its motion about the center of the galaxy. However, for practical purposes, either of these two bodies may be used to define an inertial frame.
+¿Cómo se puede estar seguro de que un marco de referencia es inercial o no lo es? Verificando si es válida la primera ley de Newton. De esta forma , la primera ley de Newton sirve como definición de los marcos de referencia inerciales.
+El espacio y el tiempo son conceptos fundamentales de la Mecánica : a cada tiempo , la posición de una partícula está determinada por una terna de números reales que son su vector posición r (t) = (x,y,z).
La forma más simple de definir estos números es mediante coordenadas cartesianas con respecto a un origen y unos ejes ortogonales , que constituyen un sistema de referencia.
Dado un sistema de referencia , las coordenadas cartesianas no son las únicas posibles para determinar los tres parámetros espaciales de la posición de una partícula. Se pueden usar coordenadas polares (en el plano ), esféricas, cilíndricas, ...las que convenga.
+En Dinámica existen dos tipos de sistemas de referencia : los sistemas inerciales y los no inerciales.
a) Sistemas inerciales: Un sistema es inercial cuando está en reposo o tiene movimiento rectilíneo y uniforme. Para un sistema inercial son válidas las leyes de Newton. En un sistema inercial solamente producen aceleración las fuerzas reales.
b)Sistemas no inerciales: Un sistema no inercial es aquel que tiene aceleración. Para que se cumplan las Leyes de Newton en estos sistemas hay dos soluciones:
1.- Suponer que los efectos de la aceleración del sistema son despreciables, cosa imposible en muchos casos.
2.- Introducir unas fuerzas ficticias o inerciales causantes de esa aceleración.
En un sistema de referencia inercial se cumple la primera ley de Newton. Por ejemplo, un tren que se mueve en línea recta a velocidad constante es un sistema de referencia inercial , ya que en él , un cuerpo en reposo permanecerá en reposo , y una canica que se deslice sobre un vidrio sin fricción , se moverá en línea recta a velocidad constante con respecto al tren , independientemente de la velocidad del tren. Ver figura M-45.
Un sistema será inercial sí y solo sí los cambios en el estado de movimiento de un cuerpo, registrados desde dicho sistema, se corresponden con interacciones (fuerzas) sobre el objeto.
De acuerdo a lo antes expuesto, podemos afirmar que la familia de sistemas inerciales es única y es en cada uno de sus integrantes que son válidas las leyes de Newton. Sin embargo, resulta extremadamente difícil identificar uno de sus miembros.
+Una reflexión debida a ALBERT EINSTEIN, en la Conferencia del Nóbel, 1911, pone de manifiesto la casi imposible tarea de encontrar un sistema verdaderamente inercial. “¿Cuál es la justificación de nuestra preferencia por los sistemas inerciales frente a todos los demás sistemas de referencia?, preferencia que parece estar sólidamente establecida sobre experiencias basadas en el principio de inercia. La vulnerabilidad del principio de inercia está en el hecho de que requiere un razonamiento que es un círculo vicioso: Una masa se mueve sin aceleraciones si está lo suficientemente alejada de otros cuerpos; pero sólo sabemos que está suficientemente alejada de otros cuerpos cuando se mueve sin aceleración”.
“El observador que hace las medidas correctas es aquel cuyo sistema de referencia es inercial”. Sin embargo, esto no resuelve en nada nuestro problema, pues la identificación de un sistema verdaderamente inercial es una tarea tan difícil como la de aislar un cuerpo del resto del universo.
Generalmente, en nuestra vida diaria, y despreciando algunos efectos, usamos la superficie de la tierra como un sistema inercial. Sin embargo, esto es sólo una aproximación, ya que dicha superficie acelera con relación al centro, y a su vez, este último, mantiene una aceleración con respecto al sol, el cual, sabemos, se mueve con relación a las estrellas lejanas, las que consideramos fijas, y éstas, giran en torno al centro de la galaxia, estando, esta última, en movimiento con respecto a otras galaxias. Como vemos es bastante difícil la elección de un sistema inercial “puro”.
La figura M-46 muestra cómo podemos usar la primera Ley de Newton para entender lo que sentimos al viajar en un vehículo que acelera. En la figura M-46-a , un vehículo está inicialmente en reposo y comienza a acelerar hacia la derecha. Una pasajera en patines (que casi eliminan los efectos de la fricción) prácticamente no tiene fuerza neta actuando sobre ella ; por lo tanto , tiende a seguir en reposo relativo al marco de referencia inercial de la Tierra. Al acelerar el vehículo a su alrededor , la pasajera se mueve hacia atrás con respecto al vehículo. Del mismo modo , una pasajera en un vehículo que está frenando tiende a seguir moviéndose con velocidad constante relativa a la Tierra , por lo que esta pasajera se mueve hacia adelante con respecto al vehículo ( ver figura M-46-b). Un vehículo también acelera si se mueve con rapidez constante pero da vuelta (ver figura M-46-c). En este caso , la pasajera tiende a seguir moviéndose con rapidez constante en línea recta relativa a la Tierra ; con respecto al vehículo , la pasajera se mueve hacia el exterior de la vuelta.



En los casos de la figura M-46 , un observador en el marco de referencia del vehículo podría concluir que hay una fuerza neta que actúa sobre la pasajera , ya que la velocidad de ésta relativa al vehículo cambia en cada caso. Esto no es correcto ; la fuerza neta sobre la pasajera es cero. El error del observador es tratar de aplicar la primera ley de Newton en el marco de referencia del vehículo , que no es inercial y en el cual dicha ley no es válida (figura M-47).

Respecto a la figura M-47 , podemos afirmar lo siguiente:
Desde el marco de referencia de este automóvil , parece que una fuerza empuja hacia adelante a los maniquíes para pruebas de choque , cuando el automóvil se detiene repentinamente. Sin embargo , tal fuerza no existe realmente : al detenerse el vehículo , los maniquíes se siguen moviendo hacia adelante como consecuencia de la primera ley de Newton.
FRAME OF REFERENCE:
*Un marco de referencia es una perspectiva desde la cual se observa un sistema. Un marco de referencia puede ser inercial o puede moverse a velocidad constante. A veces es más sencillo analizar fenómenos desde un marco de referencia en movimiento.
A frame of reference is a perspective from which a system is observed. A frame of reference may be stationary or it may move at constant velocity. It is sometimes simpler to analyzer phenomena from a moving reference frame.
* Como un ejemplo simple, imagina que estás parado en una esquina de la calle y el autobús te pasa. En su marco de referencia estacionario, un pasajero sentado en el autobús se mueve con la misma velocidad que el autobús. Sin embargo, el conductor del autobús puede observar al pasajero desde un marco de referencia móvil "anclado" al autobús. En el marco de referencia del autobús en movimiento, el conductor ve al pasajero sentado quieto.
As a simple example, imagine that you are standing on a street corner and bus passes you. In your stationary frame of reference, a passenger sitting on the bus is moving with the same velocity as the bus. However, the bus driver may observe the passenger from a moving reference frame "anchored" to the bus. In the moving bus reference frame, the driver sees the passenger sitting still.
*Evidentemente, la velocidad V' ("v-prima") de un objeto visto desde un marco de referencia en movimiento se encuentra restando Vframe, la velocidad del marco en movimiento, de V, la velocidad del objeto en relación con un marco de referencia estacionario o "de laboratorio":
Evidently, the velocity V´ ("v-prime") of an object viewed from a moving reference frame is found by subtracting Vframe, the velocity of the moving frame, from V, the velocity of the object relative to a stationary, or "laboratory" reference frame:

Un cambio de marco de referencia a menudo hace que un problema sea mucho más fácil de analizar, o reduce el problema a uno que ya ha analizado.
A change of reference frame often makes a problem much simpler to analyze, or reduces the problem to one you’ve already analyzed.
*Cuando enunciamos la ley de la inercia debemos indicar con respecto a quién o a qué se refiere el movimiento de la partícula libre. Suponemos que el movimiento de la partícula está relacionado a un observador quien es asimismo una partícula libre (o un sistema) ; es decir , que no está sujeto a interacciones con el resto del mundo. Tal observador se denomina observador inercial , y el sistema de referencia que él utiliza se llama un sistema inercial de referencia. Su ponemos que los sistemas inerciales de referencia no están rotando , debido a que la existencia de rotaciones implicaría que hay aceleraciones (o cambios en la velocidad debido a cambios en la dirección) , y entonces que hay interacciones , lo cual sería contrario a nuestra definición del observador inercial como "partícula libre" o sin aceleración. De acuerdo a la ley de la inercia , diferentes observadores inerciales pueden estar en movimiento, unos con relación a otros, con velocidad constante. Estando sus observaciones relacionadas , ya sea mediante las transformaciones de Galileo o las de Lorentz , dependiendo ello de la magnitud de sus velocidades relativas.
When we state the law of inertia, we must indicate to whom or what the motion of the free particle is referred. We assume that the motion of the particle is relative to an observer who is himself a free particle (or system), i.e., who is not subject to interactions with the rest of the world. Such an observer is called an inertial observer, and the frame of reference he uses is called an inertial frame of reference. We assume that inertial frames of reference are not rotating, because the existence of rotations would imply that there are accelerations (or changes in velocity due to changes in direction), and therefore that there are interactions, which would be contrary to our definition of the inertial observer as being a “free particle”, or one without acceleration. According to the law of inertia, different inertial observers may be in motion, relative to each other, with constant velocity. Therefore, their observations are correlated through either the Galilean or the Lorentz transformation, depending on the magnitude of their relative velocities.
*Un enunciado equivalente de la primera ley de Newton es que si sobre un objeto no actúan fuerzas , o si la suma total de las fuerzas que actúan sobre el objeto es nula, entonces
(1) un objeto en reposo sigue en reposo y
(2) un objeto en movimiento sigue moviéndose con velocidad constante.
Newton's first law of motion: If there is no force on an object, or if there is no net force when two or more forces act on the object, then
1) an object at rest remains at rest, and
2) an object in motion continues to move with constant velocity.
*Usaremos el término "popper" para referirnos a un lanzador vertical de bolas.
A primera vista, puede parecer que la primera ley de Newton (un objeto en reposo permanece en reposo y un objeto en movimiento permanece en movimiento a menos que actúe sobre ella una fuerza neta) está contenida dentro de la segunda ley de Newton. En realidad, este no es el caso. La primera ley es también una declaración con respecto a los marcos de referencia. Esta es la información NO contenida en la segunda ley. A veces, la primera ley también se llama la ley de la inercia. Define un cierto conjunto de marcos de referencia en los que se sostiene la primera ley, y estos marcos de referencia se denominan por lo tanto marcos de referencia inerciales. Dicho de otra manera, la primera ley de Newton establece que si la fuerza neta sobre un objeto es cero, es posible encontrar al menos un marco de referencia en el que ese objeto sea estacionario. Hay muchos fotogramas en los que el objeto se mueve con una velocidad constante. Un popper de bola en un carro (no se muestra a escala) se muestra moviéndose en una pista en tres animaciones diferentes (la posición se da en metros y el tiempo se da en segundos). En cada animación la bola es expulsada hacia arriba por el mecanismo popper en t = 1 s. Reiniciar. Consideremos primero la Animación 1. En esta animación el carro está parado. Pero, ¿lo es realmente? Sabemos que no podemos saber si estamos estacionarios o moviéndonos a una velocidad constante (en otras palabras, en un marco de referencia inercial). Recordemos que si nos estamos moviendo en relación con la Tierra a una velocidad constante estamos en un marco de referencia inercial. Entonces, ¿cómo podemos saber si nos estamos moviendo? ¿Qué tal el carrito? No podemos decir si hay movimiento mientras el movimiento relativo con respecto a la Tierra pueda describirse por una velocidad constante. En la Animación 1 el carro podría estar parado. En este caso, esperamos, y realmente vemos, que la bola vuelva a entrar en el popper. Sin embargo, si el carro se moviera en relación con la Tierra y nos estuviéramos moviendo junto con el carro, ¡el movimiento de la pelota y el carro se vería exactamente igual! ¿Cómo sería el movimiento de esta bola y carro si el carro se moviera en relación con nuestro marco de referencia (o si nos movimos en relación con su marco de referencia)? Las animaciones 2 y 3 muestran el movimiento de diferentes marcos de referencia. ¿Cómo son estas animaciones? Ambas animaciones se asemejan al movimiento del proyectil. El movimiento de la pelota se parece al movimiento en un plano en lugar del movimiento en una línea. ¿La bola sigue aterrizando en el popper? ¿Esperarías esto? Seguro. Aquí no hay nada fuera de lo común. Dado que no hay fuerzas en la dirección x, el movimiento de la bola (y el carro) debe describirse por velocidad constante en esa dirección. Por lo tanto, la bola y el carro tienen la misma velocidad horizontal constante.
We will use the term popper to refer to a vertical ball thrower.
On first glance it may seem like Newton's first law (an object at rest remains at rest and an object in motion remains in motion unless acted on by a net force) is contained within Newton's second law. This is actually not the case. The first law is also a statement regarding reference frames. This is the information NOT contained in the second law. Sometimes the first law is also called the law of inertia. It defines a certain set of reference frames in which the first law holds, and these reference frames are therefore called inertial frames of reference. Put another way, Newton's first law states that if the net force on an object is zero, it is possible to find at least one reference frame in which that object is stationary. There are many frames in which the object is moving with a constant velocity. A ball popper on a cart (not shown to scale) is shown moving on a track in three different animations (position is given in meters and time is given in seconds). In each animation the ball is ejected straight up by the popper mechanism at t = 1 s. Restart. Let us first consider Animation 1. In this animation the cart is stationary. But is it really? We know that we cannot tell if we are stationary or moving at a constant velocity (in other words in an inertial reference frame). Recall that if we are moving relative to Earth at a constant velocity we are in an inertial reference frame. So how can we tell if we are moving? How about the cart? We cannot tell if there is motion as long as the relative motion with respect to Earth can be described by a constant velocity. In Animation 1 the cart could be stationary. In this case, we expect—and actually see—that the ball lands back in the popper. However, if the cart was moving relative to Earth and we were moving along with the cart, the motion of the ball and the cart would look exactly the same! What would the motion of this ball and cart look like if the cart moved relative to our reference frame (or if we moved relative to its reference frame)? Animations 2 and 3 show the motion from different reference frames. What do these animations look like? Both animations resemble projectile motion. The motion of the ball looks like motion in a plane as opposed to motion on a line. Does the ball still land in the popper? Would you expect this? Sure. There is nothing out of the ordinary going on here. Since there are no forces in the x direction, the motion of the ball (and cart) should be described by constant velocity in that direction. Therefore the ball and the cart have the same constant horizontal velocity.






Cinemagrafías provenientes de Physlets. Animación 1.
Cinemagraphs coming from Physlets. Animation 1.
-------------------------------------------------------------------------------------------------------








Cinemagrafías provenientes de Physlets. Animación 2.
Cinemagraphs coming from Physlets. Animation 2.
-------------------------------------------------------------------------------------------------








Cinemagrafías provenientes de Physlets. Animación 3.
Cinemagraphs coming from Physlets. Animation 3.
-------------------------------------------------------------------------------------------------------
* La primera ley se cumple en esta forma sólo para medidas efectuadas por determinados observadores. Una chica montada en un tiovivo (carrusel) ve objetos que sin estar sometidos a ninguna fuerza experimentan movimientos bastante complicados , mientras que un chico que permanezca quieto sobre el suelo los ve en reposo o moviéndose con velocidad constante. Por lo tanto, la primera ley de Newton , tal como la hemos enunciado , es válida para el chico que está en reposo, pero no para la chica. La clave está en que la chica está sometida a aceleración, ya que su velocidad está cambiando , y la primera ley de Newton, tal como la hemos establecido, no es válida para un observador que se acelere. Ver figura M-48.
The first law holds true in the form stated only for measurements made by certain observers. A girl riding on a merry-go-round sees objects not subjected to any net force undergo rather complex motions, while a boy at rest on the ground sees them at rest or moving with constant velocity. Thus, Newton's first law as stated is true for the boy at rest but not for the girl. The point is that the girl is accelerating, since her velocity is changing, and Newton's first law as stated does not hold true for someone who is accelerating. See figure M-48.
*La primera ley nos lleva a definir un sistema de coordenadas inercial o sistema de referencia inercial como aquel en que se cumple la primera ley de Newton. Estrictamente hablando, el chico del ejemplo (figura M-48) no está en un sistema totalmente inercial ya que se halla sobre la Tierra, que efectúa diariamente una rotación sobre su eje , gira alrededor del Sol anualmente y se mueve con el sistema solar respecto a las estrellas muy lejanas. Generalmente, estos efectos pueden despreciarse y se puede tratar a la Tierra como un sistema inercial. Sin embargo, la rotación diaria de la Tierra afecta a los movimientos de gran escala de la atmósfera y los océanos.
The first law leads us to define an inertial coordinate system or reference frame as one in which Newton's first law holds true as stated. Strictly speaking, the boy in the example (figure M-52) is not quite in an inertial frame, since he is standing on the earth, which is revolving daily on its axis, rotating annually about the sun, and moving with the solar system relative to the distant stars. Usually, these effects can be ignored, and the earth can be treated as an inertial frame. However, the earth 's daily revolution does affect the large-scale motions of the atmosphere and the oceans.
*Un sistema de coordenadas que se mueve a velocidad constante respecto a un sistema inercial , es a su vez un sistema inercial. Para comprender esto , consideremos un observador que se encuentra parado en la carretera y otro observador en un coche que se mueve a velocidad constante. Si ambos observadores miden la velocidad de un objeto móvil , sus medidas diferirán en una constante , que es su velocidad relativa. Así pues , estarán de acuerdo en si el objeto está acelerado o no, y la primera ley de Newton será igualmente válida para los dos observadores.
A coordinate system moving at a constant velocity relative to an inertial frame is itself an inertial frame. To see this, consider an observer standing on the ground and another in a car moving at a constant velocity. If both observers measure the velocity of a moving object, their measurements will differ by their constant relative velocity. Hence, they will agree on whether the motion of the object is accelerated, and Newton's first law will work equally well for both observers.
*Tras esta explicación, vemos que los coches y los aviones que se mueven a velocidad constante con respecto al suelo son sistemas de referencia inerciales , mientras que los vehículos acelerados , como los tiovivos (carruseles) y los columpios , no lo son. Para mayor claridad, consideremos el conductor de un coche acelerado, quien nota que el respaldo de su asiento ejerce una fuerza sobre él. Respecto al suelo está acelerado, pero respecto al coche no. La primera ley de Newton concuerda con las medidas de un observador en reposo en el suelo: el estado de movimiento del conductor está siendo cambiado por fuerzas que actúan sobre él. La primera ley de Newton no es válida en el sistema de referencia del coche acelerado ya que existe una fuerza sobre el conductor , aunque éste permanece en reposo.
From this discussion, we see that cars or airplanes moving at constant velocities relative to the ground are inertial reference frames, while accelerating vehicles, merry-go-rounds, and playground swings are not. As a further illustration, consider the driver of an accelerating car. She feels the back of her seat exerting a force on her. Relative to the ground, she is accelerating, but relative to the car, she is not. The first law is consistent with the measurements of an observer at rest on the ground: the state of motion of the driver is being changed by forces acting on her. The first law does not work in the frame of the accelerating car, since there is a force on the driver, but she remains at rest.
*¿Cómo se puede estar seguro de que un marco de referencia es inercial o no lo es? Verificando si es válida la primera ley de Newton. De esta forma, la primera ley de Newton sirve como definición de los marcos de referencia inerciales.
How can we be sure a reference frame is inertial or not? By checking to see if Newton's first law holds. Thus, Newton's first law serves as the definition of inertial reference frames.

+Según la Real Academia Española, el significado de gnomo es el siguiente:
Gnomo: En los cuentos infantiles, geniecillo o enano.
+Jammer (1998, 2000) expresó lo siguiente: Imaginemos un minúsculo gnomo que está sentado sobre una bola que gira por efecto de una cuerda ligada a un eje que da vueltas. Supongamos asimismo que el gnomo está unido a la bola de un modo idealmente rígido, para incluir la objeción anterior, y que no se da rozamiento alguno con el aire que le pueda informar de su estado de movimiento. Como este pequeño observador conoce las leyes de Newton y a su juicio nada hay que le indique su movimiento, podría considerar con todo derecho que se halla en reposo o en movimiento inercial. Sin embargo el gnomo ve la cuerda tensa a causa del giro, y como él se supone quieto ha de postular la existencia de una fuerza que compense la tensión de la cuerda, de manera que la suma final de todas las fuerzas sea nula y se garantice su suposición inicial. Este es el genuino sentido de las fuerzas de inercia: asegurar el cumplimiento formal de las leyes de Newton en sistemas de referencia acelerados a los cuales, en rigor, dichas leyes no corresponden.
Panorama general de las leyes del movimiento de Newton (primer comentario)
Overview of Newton's Laws of Motion (first comment)
*Las dos primeras leyes establecen las interrelaciones cuantitativas de espacio, tiempo, materia y movimiento. La tercera ley viene a dar una coherencia definitiva a las dos primeras, estableciendo la idea de interacciones mutuas de los cuerpos materiales. Establece una unidad del mundo material al atribuir una acción recíproca entre los cuerpos materiales que provoca sus diferentes estados de movimiento, desechando la concepción del mundo como una simple suma de objetos y fenómenos dispersos y desligados entre sí (Álvarez, 2002).
The first two laws establish the quantitative interrelationships of space, time, matter, and motion. The third law comes to give a definitive coherence to the first two, establishing the idea of mutual interactions of material bodies. It establishes a unity of the material world by attributing a reciprocal action between the material bodies that provokes their different states of movement, discarding the conception of the world as a simple sum of objects and phenomena dispersed and disconnected from each other (Álvarez, 2002).
EL PRINCIPIO DE INVARIANCIA
THE PRINCIPLE OF INVARIANCE
*Algunas cantidades como la masa, la fuerza, el tiempo y la aceleración son invariantes, lo que significa que tienen los mismos valores numéricos cuando se miden en diferentes marcos de referencia inerciales. Otras cantidades como la velocidad, la energía cinética y el trabajo tienen diferentes valores en diferentes marcos inerciales. Sin embargo, las leyes de la física tienen la misma forma en todos los marcos de referencia inerciales. Esto se llama el principio de invariancia.
Some quantities such as mass, force, time, and acceleration are invariant, which means that they have the same numerical values when measured in different inertial frames of reference. Other quantities such as velocity, kinetic energy, and work have different values in different inertial frames. However , the laws of physics have the same form in all inertial frames of reference. This is called the principle of invariance.

Figura M-49. Figure M-49
*El niño está tirando el agua lanzando el cubo hacia adelante. Si se detiene, el agua continuará su movimiento a lo largo de una línea recta. Sin embargo, debido a la fuerza de la gravedad, sigue un camino parabólico.
The boy is throwing the water out by pitching the bucket forward. If he stops, the water will continue its motion along a straight line. However, because of the force of gravity, it follows a parabolic path.
----------------------------------------------------------------------------------------------------
*La primera ley de Newton no explica lo que sucede con un objeto con fuerza neta cero, esto es, múltiples fuerzas que se cancelan; expresa lo que ocurre en ausencia de fuerzas externas. Esta diferencia sutil pero importante permite definir la fuerza como la causa de un cambio en el movimiento. La descripción de un objeto bajo el efecto de fuerzas que se equilibran la cubre la segunda ley de Newton.
Newton’s first law does not say what happens for an object with zero net force, that is, multiple forces that cancel; it says what happens in the absence of external forces. This subtle but important difference allows us to define force as that which causes a change in the motion. The description of an object under the effect of forces that balance is covered by Newton’s second law.
*Desde el marco de referencia de este automóvil, parece que una fuerza empuja hacia adelante a los maniquíes para pruebas de choque, cuando el automóvil se detiene repentinamente. Sin embargo, tal fuerza no existe realmente: al detenerse el vehículo, los maniquíes se siguen moviendo hacia adelante como consecuencia de la primera ley de Newton (figura M-51).
From the frame of reference of the car, it seems as though a force is pushing the crash test dummies forward as the car comes to a sudden stop. But there is really no such force: As the car stops, the dummies keep moving forward as a consequence of Newton’s first law (figure M-51).
*Claramente, en la mayoría de los casos, es más fácil trabajar en un marco inercial de referencia para que pueda utilizar las leyes del movimiento de Newton. Sin embargo, si un físico decide trabajar en un marco de referencia no inercial y todavía aplicar las leyes del movimiento de Newton, es necesario invocar cantidades hipotéticas que a menudo se denominan fuerzas ficticias: efectos inerciales que se perciben como "fuerzas" en marcos no inerciales de referencia, pero no existen en marcos de referencia inerciales.
Clearly, in most cases, it is easier to work in an inertial frame of reference so that you can use Newton’s laws of motion. However, if a physicist chooses to work in a non-inertial frame of reference and still apply Newton’s laws of motion, it is necessary to invoke hypothetical quantities that are often called fictitious forces: inertial effects that are perceived as “forces” in non-inertial frames of reference, but do not exist in inertial frames of reference.
-----------------------------------------------------------------------------------------------------------------
FRANK: "Es muy útil caminar sabiendo hacia qué destino vamos."
ORYX: "Eso es obvio."
FRANK: "En nuestro proceso de aprendizaje del presente capítulo debes ser capaz de resolver , entre otras, la siguiente actividad. Me refiero a la actividad semiguiada Nº 01. A continuación, te presento un adelanto de lo que haremos juntos. En la actividad semiguiada Nº 01 los estudiantes demostrarán sus conocimientos científicos de manera parcial , pues yo los guiaré de manera parcial. En el presente capítulo hay más actividades pero ésta es una de las más importantes."
ORYX: "Excelente."

Ideas básicas sobre las fuerzas:
La mecánica es la disciplina que describe y estudia las posiciones de los cuerpos y sus variaciones en el tiempo en función de sus interacciones recíprocas. Las variables mecánicas típicas son las posiciones y las velocidades, pero también las formas y deformaciones de los cuerpos, que son posiciones y cambios de posición relativos entre puntos de un cuerpo. Las acciones mecánicas son las que afectan a este tipo de variables, y ellas tienen lugar cuando un cuerpo, por medio de la aplicación de fuerzas, empuja, mueve o deforma a otro.
La primera noción básica que dejaremos establecida es que, en nuestro modelo de las interacciones mecánicas, la fuerza debe ser un ente de naturaleza vectorial, porque es lo que se aplica a un cuerpo para producir desplazamientos, que son vectores. Esto es cierto tanto si hablamos de poner en movimiento como de deformar algo. En ambos casos lo que se logra se expresa con vectores de desplazamiento, y para lograrlo en los dos casos se debe aplicar una fuerza que, por lo tanto, debe gozar de la misma posibilidad de ser orientada en el espacio que los desplazamientos que tiende a producir.
Alemañ (2009) expresó que la fuerza, masa o energía son nociones que carecen de definición por el sencillo hecho de ser conceptos primitivos, y por ello indefinibles. Manifestó que los indefinibles por su misma naturaleza −como sillares sobre los cuales construimos el resto de nuestro conocimiento− no admiten definición.
Mosquera (2012) hace referencia a Feynman (1971) quien expresó que el concepto de fuerza es muy intuitivo y que se le reconoce como la causa de que un cuerpo cambie su estado de movimiento al proporcionarle una aceleración. De manera que si un cuerpo se encontraba detenido pasará a moverse y si estaba moviéndose a cierta velocidad constante pasará a moverse más rápido, más lento o a detenerse:
“si insisten en una definición precisa de fuerza, ¡nunca la tendrán! Primero, porque la segunda ley de Newton no es exacta, y segundo, porque para comprender las leyes físicas deben comprender que todas son alguna forma de aproximación”
Entonces, de acuerdo a lo anterior, trataremos de seguir tratando el concepto de fuerza a nivel intuitivo, desde luego, apoyado en los trabajos de Newton, pero haciendo la aclaración de que las expresiones matemáticas que intentan modelar algún fenómeno físico, no pueden funcionar a la perfección en el ámbito real, pues es muy difícil controlar (o conocer) todas las variables que intervienen en nuestro entorno natural.
Fuerzas fundamentales de la naturaleza:
Interacción gravitatoria:
La fuerza gravitatoria o gravitacional es la fuerza de atracción que se presenta entre dos cuerpos debido a sus masas; en teoría su alcance es ilimitado. Esta fuerza es universal, ya que no sólo nos sujeta a la superficie de la Tierra, sino que además mantiene a los planetas en sus órbitas alrededor del Sol. Debido a esta fuerza, cada objeto atrae al resto de los objetos del Universo.
Interacción electromagnética:
*Es la responsable de las interacciones entre algunas de las partículas elementales que componen la materia. Por ejemplo, proporciona la fuerza de atracción que mantiene a los electrones cerca de los protones en el átomo. Esta fuerza se debe a la propiedad de la materia llamada carga eléctrica; puede ser atractiva o repulsiva. Como lo indica su nombre, la fuerza electromagnética incluye las fuerzas magnética y eléctrica. El alcance de dicha fuerza es ilimitado.
*Aparece en objetos magnetizados o con carga eléctrica.
*Permite describir la radiación electromagnética.
Interacción nuclear fuerte:
La fuerza nuclear fuerte es la responsable de que los protones y neutrones permanezcan unidos en el núcleo del átomo. Sin esta fuerza los núcleos no existirían. Es la fuerza fundamental más intensa que se encuentra en la naturaleza. El alcance de esta fuerza es limitado, ya que no actúa fuera del núcleo.
Interacción nuclear débil:
*Responsable de las desintegraciones βde núcleos radiactivos y de todos los procesos entre partículas elementales donde intervienen neutrinos.
*Debido al control que ejerce esta fuerza en las reacciones nucleares que ocurren en el Sol, determina la vida media de éste.
*Nuclear débil + electromagnética ⇒ electrodébil. En la tabla M- se muestra una comparación entre las fuerzas fundamentales. A continuación una interesante lectura que nos permite ampliar nuestros conocimientos.
La fuerza resulta de una interacción:
En nuestro modelo es esencial considerar que las fuerzas no son propiedades de un cuerpo, sino que son resultado de una interacción entre cuerpos. Excepto el caso especial de la atracción gravitatoria, que analizaremos aparte, la interacción requiere de una zona de contacto a través de la cual cada cuerpo aplica fuerza al otro. Debe estar claro que, dejando de lado la acción de la gravedad, o sea el “peso” del cuerpo, todas las demás fuerzas son de contacto: no hay fuerza donde no hay contacto. Será posible identificar todas las fuerzas actuantes sólo si se revisan todos los contactos.
Y esto implica dos cosas muy simples que deberemos respetar:
a) Cuando termina el contacto, deja de aplicarse la fuerza. Esto significa que un cuerpo no conserva la fuerza que se le aplicó: conserva energía, conserva movimiento, pero no puede conservar fuerza. Llamamos fuerza a cierta propiedad del contacto no a algo que el cuerpo pueda acumular y conservar.
Es decir, si impulsamos un cuerpo aplicándole una fuerza F , y después de que dejamos de empujarlo continúa moviéndose, entendemos que eso es la inercia, y no que lo hace porque conserva la fuerza que le hemos aplicado. El cuerpo conserva el movimiento que le hemos comunicado aplicándole fuerza. Si se nos pregunta qué fuerza está actuando sobre el cuerpo en ese momento (después de que dejamos de empujarlo), no debemos decir que sigue actuando F , porque eso significaría que lo seguimos empujando.
b) Un cuerpo no se aplica fuerza a sí mismo. La fuerza sobre un cuerpo sólo puede ser aplicada por otro cuerpo, al cual frecuentemente llamaremos “agente exterior”, para destacar este concepto fundamental.
Esto significa que un cuerpo aislado no se puede poner en movimiento, ni frenarse, a sí mismo. La física no admite la posibilidad de que un cuerpo o ser adquiera movimiento (o se frene), al estilo “Superman”, recurriendo a una especie de “fuerza interior”. Un automóvil, por caso, sólo puede iniciar su movimiento, o frenarse, aplicando fuerza al piso. No podría hacerlo sin contacto con el piso. Insistiremos y reflexionaremos mucho más sobre esto oportunamente.
Efecto de las fuerzas sobre los movimientos:



Por acción de un agente externo que no se muestra, una fuerza tranversal desvía al cuerpo. Según el principio de inercia éste seguiría en línea recta si no le aplicaran fuerzas, y eso es lo que ocurre cuando el agente suspende su acción.
------------------------------------------------------------------------------------------------------
*Vamos a plantear cuál es el efecto de una fuerza sobre el movimiento de un cuerpo. Uno de los casos más simples o elementales posibles es: un cuerpo sobre el que se aplica una única fuerza.
*Para que este planteo no sea mal interpretado, imaginaremos un cuerpo aislado, muy lejos de la influencia gravitatoria de cualquier planeta, y sin contacto con cosa alguna; diremos que está como flotando en la nada (no hay gravedad, no hay piso, no hay aire, no hay rozamiento, etc.).
*Así que para este hipotético cuerpo que, según el principio de inercia, mientras no se le apliquen fuerzas mantendrá su reposo o movimiento uniforme en línea recta, podremos decir:
1. Si el cuerpo está en reposo y se le aplica una (única) fuerza, iniciará el movimiento con la orientación dela fuerza. Si la fuerza se mantiene aplicada con la misma orientación, la velocidad aumentará mientras ello ocurra. Si la fuerza deja de aplicarse, la velocidad dejará de aumentar, pero no disminuirá. Para que disminuya se necesita una fuerza que lo frene.
2. Si el cuerpo está en movimiento y se le aplica una fuerza orientada en sentido contrario al movimiento, el efecto será la disminución de la velocidad, pudiendo llegar a detener el cuerpo.
3. Si el cuerpo está en movimiento y se le aplica una fuerza transversal, su efecto será desviar al cuerpo de la línea recta que seguiría naturalmente. La desviación ocurre, por supuesto, en el sentido de la fuerza aplicada, y el cuerpo describe una línea curva mientras dura la aplicación de la fuerza.
4. Si se aplican varias fuerzas simultáneamente sobre un cuerpo, el efecto sobre el movimiento es la superposición de los efectos que ellas tendrían por separado. Como veremos pronto, en estos casos se determina la fuerza resultante, que puede pensarse como la fuerza neta actuante, y se razona con ella como si fuese la única fuerza.
Naturaleza vectorial de las fuerzas y principio de superposición
La Regla del Equilibrio
The Equilibrium Rule
*Si con un cordón atas una bolsa con 2 libras de azúcar y la cuelgas de una báscula de mano (ver figura), el resorte de la báscula se estirará hasta que ésta indique 2 libras. El resorte estirado está bajo una “fuerza de estiramiento” llamada tensión. Es probable que la misma báscula en un laboratorio científico indique que la misma fuerza es 9 newtons. Tanto las libras como los newtons son unidades de peso, que a su vez son unidades de fuerza. La bolsa de azúcar es atraída hacia la Tierra con una fuerza gravitacional de 2 libras, o lo que es igual, de 9 newtons. Si cuelgas dos bolsas de azúcar iguales a la primera, la lectura será 18 newtons.
If you tie a string around a 2-pound bag of sugar and hang it on a weighing scale (see figure), a spring in the scale stretches until the scale reads 2 pounds. The stretched spring is under a "stretching force" called tension. The same scale in a science lab is likely calibrated to read the same force as 9 newtons. Both pounds and newtons are units of weight, which in turn are units of force. The bag of sugar is attracted to Earth with a gravitational force of 2 pounds-or, equivalently, 9 newtons. Hang twice as much sugar from the scale and the reading will be 18 newtons.
*Nota que aquí son dos las fuerzas que actúan sobre la bolsa de azúcar: la fuerza de tensión que actúa hacia arriba, y su peso que actúa hacia abajo. Las dos fuerzas sobre la bolsa son iguales y opuestas y se anulan; la fuerza neta es cero. Por consiguiente la bolsa permanece en reposo. De acuerdo con la primera ley de Newton ninguna fuerza neta actúa sobre la bolsa. Podemos ver la primera ley de Newton con una luz diferente: el equilibrio mecánico.
Note that there are two forces acting on the bag of sugar-tension force acting upward and weight acting downward. The two forces on the bag are equal and opposite, and they cancel to zero. Hence, the bag remains at rest. In accord with Newton's first law, no net force acts on the bag. We can look at Newton's first law in a different light-mechanical equilibrium.
*Cuando la fuerza neta que actúa sobre algo es cero, se dice que ese algo está en equilibrio mecánico. En notación matemática, la regla del equilibrio es
When the net force on something is zero, we say that something is in mechanical equilibrium." In mathematical notation, the equilibrium rule is
Fuerza de soporte
Support force
*Imagina un libro que yace sobre una mesa. Está en equilibrio. ¿Qué fuerzas actúan sobre él? Una es la que se debe a la gravedad y que es el peso del libro. Como el libro está en equilibrio, debe haber otra fuerza que actúa sobre él que haga que la fuerza neta sea cero: una fuerza hacia arriba, opuesta a la fuerza de gravedad. La mesa es la que ejerce esa fuerza hacia arriba. A esta fuerza se le llama fuerza de soporte. Esta fuerza de soporte, hacia arriba, a menudo se llama fuerza normal y debe ser igual al peso del libro. Si a la fuerza normal la consideramos positiva, el peso es hacia abajo, por lo que es negativo, y al sumarse las dos resulta cero. La fuerza neta sobre el libro es cero. Otra forma de decir lo mismo es
Consider a book lying at rest on a table. It is in equilibrium. What forces act on the book? One force is that due to gravity-the weight of the book. Since the book is in equilibrium, there must be another force acting on the book to produce a net force of zero-an upward force opposite to the force of gravity. The table exerts this upward force. We call this the upward support force. This upward support force, often called the normal force, must equal the weight of the book.f If we call the upward force positive, then the downward weight is negative, and the two add to become zero. The net force on the book is zero. Another way to say the same thing is
*Para entender mejor que la mesa empuja el libro hacia arriba, compara el caso de la compresión de un resorte (ver figura ). Comprime el resorte hacia abajo, y podrás sentir que el resorte empuja tu mano hacia arriba. Asimismo, el libro que yace sobre la mesa comprime los átomos de ésta, que se comportan como resortes microscópicos. El peso del libro comprime a los átomos hacia abajo, y ellos comprimen el libro hacia arriba. De esta forma los átomos comprimidos producen la fuerza de soporte.
To understand better that the table pushes up on the book, compare the case of compressing a spring (see figure ). If you push the spring down, you can feel the spring pushing up on your hand. Similarly, the book lying on the table compresses atoms in the table, which behave like microscopic springs. The weight of the book squeezes downward on the atoms, and they squeeze upward on the book. In this way, the compressed atoms produce the support force.
*Cuando te subes en una báscula de baño hay dos fuerzas que actúan sobre ella. Una es el tirón de la gravedad, hacia abajo, que es tu peso, y la otra es la fuerza de soporte, hacia arriba del piso. Estas fuerzas comprimen un mecanismo (en efecto, un resorte) en la báscula que está calibrado para indicar la magnitud de la fuerza de soporte (ver figura ). Es esta fuerza de soporte que muestra tu peso. Cuando te pesas en una báscula de baño en reposo, la fuerza de soporte y la fuerza de gravedad que te jala hacia abajo tienen la misma magnitud. Por lo tanto, decimos que tu peso es la fuerza de gravedad que actúa sobre ti.
When you step on a bathroom scale, two forces act on the scale. One is your downward push on the scale-the result of gravity pulling on you-and the other is the upward support force of the floor. These forces squeeze a mechanism (in effect, a spring) within the scale that is calibrated to show the magnitude of the support force (see figure). It is this support force that shows your weight. When you weigh yourself on a bathroom scale at rest, the support force and the force of gravity pulling you down have the same magnitude. Hence we can say that your weight is the force of gravity acting on you.
Equilibrio de cosas en movimiento
Equilibrium of Moving Things
*El reposo sólo es una forma de equilibrio. Un objeto que se mueve con rapidez constante en una trayectoria rectilínea también está en equilibrio. El equilibrio es un estado donde no hay cambios. Una bola de bolos que rueda a rapidez constante en línea recta también está en equilibrio, hasta que golpea los pinos. Si un objeto está en reposo (equilibrio estático) o rueda uniformemente en línea recta (equilibrio dinámico),
Rest is only one form of equilibrium. An object moving at constant speed in a straight-line path is also in equilibrium. Equilibrium is a state of no change. A bowling ball rolling at constant speed in a straight line is in equilibrium-until it hits the pins. Whether at rest (static equilibrium) or steadily rolling in a straight-line path (dynamic equilibrium),
*De acuerdo con la primera ley de Newton, un objeto que sólo esté bajo la influencia de una fuerza no puede estar en equilibrio. La fuerza neta no podría ser cero. Únicamente cuando actúan sobre él dos o más fuerzas puede estar en equilibrio. Podemos probar si algo está en equilibrio o no, observando si sufre cambios en su estado de movimiento o no.
It follows from Newton's first law that an object under the influence of only one force cannot be in equilibrium. Net force couldn't be zero. Only when two or more forces act on it can it be in equilibrium. We can test whether or not something is in equilibrium by noting whether or not it undergoes changes in its state of motion.
*Imagina una caja que se empuja horizontalmente por el piso de una fábrica. Si se mueve a una rapidez constante, y su trayectoria es una línea recta, está en equilibrio dinámico. Esto nos indica que sobre la caja actúa más de una fuerza. Existe otra, que es probablemente la fuerza de fricción entre la caja y el piso. El hecho de que la fuerza neta sobre la caja sea igual a cero significa que la fuerza de fricción debe ser igual y opuesta a la fuerza de empuje.
Consider a crate being pushed horizontally across a factory floor. If it moves Consider a crate being pushed horizontally across a factory floor. If it moves at a steady speed in a straight-line path, it is in dynamic equilibrium. This tells us that more than one force acts on the crate. Another force exists-likely the force of friction between the crate and the floor. The fact that the net force on the crate equals zero means that the force of friction must be equal and opposite to our pushing force.
*La regla de equilibrio, , brinda una forma razonada de observar todas las cosas en reposo: pilas de piedras, objetos de tu habitación o las vigas de acero de los puentes o en la construcción de edificios. Cualquiera que sea su configuración, en equilibrio estático, todas las fuerzas que actúan siempre se equilibran a cero. Lo mismo es cierto para los objetos que se mueven constantemente, sin acelerar, desacelerar ni cambiar de dirección. Para el equilibrio dinámico, todas las fuerzas que actúan también se equilibran a cero. La regla del equilibrio permite que veas mejor que el ojo del observador casual. Resulta agradable saber las razones de la estabilidad de los objetos en el mundo actual.
The equilibrium rule, , provides a reasoned way to view all things at rest-balancing rocks, objects in your room, or the steel beams in bridges or in building construction. Whatever their configuration, if in static equilibrium, all acting forces always balance to zero. The same is true of objects that move steadily, not speeding up, slowing down, or changing direction. For dynamic equilibrium, all acting forces also balance to zero. The equilibrium rule is one that allows you to see more than meets the eye of the casual observer. It's nice to know the reasons for the stability of things in our everyday world.
Combinando fuerzas
Combining forces
*Observamos que las fuerzas eran vectores y que cuando dos fuerzas actúan en un punto (por ejemplo, cualquier punto en una cuerda o cuerda estirada) deben ser iguales y opuestas (iguales en magnitud pero opuestas en dirección): se llaman acción y reacción; y el objeto sobre el que actúan (por ejemplo, un poco de cuerda en el punto P) no se mueve porque la acción combinada de las fuerzas es cero: están "en equilibrio" y tienen un "resultado" que es lo mismo que ninguna fuerza en absoluto.
We noted that forces were vectors and that when two forces act at a point (e.g. any point in a stretched rope or string) they must be equal and opposite (equal in magnitude but opposite in direction): they are called action and reaction; and the object on which they act (e.g. a little bit of string at point P) doesn’t move because the combined action of the forces is zero – they are ‘in balance’ and have a ‘resultant’ which is the same as no force at all.
Principales fuerzas presentes en los sistemas mecánicos

Fuerza gravitatoria o gravitacional
+Es importante comprender bien el concepto de esfera celeste. La esfera celeste puede considerarse como una esfera de radio infinito, con su centro en la ubicación del observador. En consecuencia, cuando se mira hacia el cielo, se ven los objetos celestes como si estuvieran fijos en la superficie interior de esta esfera, aunque en realidad están a distancias que varían considerablemente. Ver la figura

+Existe un evidente vínculo entre la Física y las diversas ramas de la ingeniería.
Michel Valero fue un destacado físico , ingeniero óptico e ingeniero nuclear colombiano. Uno de sus libros figura en las referencias bibliográficas del presente blog de alfabetización matemática. A continuación algunos extractos de sus enseñanzas:
+Anteriormente admitimos los conceptos de la aceleración de la gravedad y del peso sin analizar el hecho de la gravitación.
Consideremos ahora este fenómeno:
(a) Los planetas se desplazan sobre elipses cuyo foco es el Sol.
(b) La recta que une el planeta al Sol, barre áreas iguales en tiempos iguales.
(c) Los cuadrados de los períodos de los planetas son proporcionales a los cubos de las distancias medias al Sol.
En otras palabras,
(a) El movimiento de un planeta es periódico y se realiza en una órbita elíptica cerrada, en la que el Sol ocupa uno de los focos.
(b) El radio vector que va del Sol a un planeta describe áreas iguales en tiempos iguales en todas las partes de la órbita.
(c) El cuadrado del periodo o tiempo en que un planeta recorre su órbita alrededor del Sol, es proporcional al cubo del radio medio de la órbita.
+De la primera y tercera leyes, Newton dedujo su famosa ley de gravitación universal. Recíprocamente, de la ley de la gravitación, deduciremos la ley de Kepler.

"Dos partículas ejercen una sobre la otra, una fuerza de atracción dirigida sobre la línea que los una y proporcional a sus masas e inversamente proporcional al cuadrado de la distancia de las dos partículas."
+La Tierra atrae a la Luna con una fuerza de la misma naturaleza que la fuerza con que el Sol atrae a los planetas.
CAPÍTULO V: "CONSISTENCIA ENTRE LA PRIMERA Y LA SEGUNDA LEY DEL MOVIMIENTO DE NEWTON"
CHAPTER V: "CONSISTENCY BETWEEN NEWTON’S FIRST AND SECOND LAW OF MOTION"
CHAPITRE V: "COHÉRENCE ENTRE LA PREMIÈRE ET LA DEUXIÈME LOI DU MOUVEMENT DE NEWTON"
*CAPÍTULO OPTATIVO / OPTATIVE CHAPTER /CHAPITRE OPTATIF
*En este capítulo se evidenciará la consistencia entre la primera y la segunda ley del movimiento de Newton. Empezaremos con la expresión matemática de la segunda ley de Newton:
F = (m) (a)
F: fuerza, m: masa, a: aceleración
Si la fuerza es constante, la aceleración que provoca también es constante, la cual se puede obtener por:
a = V - Vo / t
V: velocidad final. Vo : velocidad inicial. t: tiempo
Combinando las dos últimas ecuaciones, se obtiene:
F = m (V - Vo / t)
Reordenando esta ecuación se tiene:
( F/ m ) t = V - Vo
Para algunos docentes de ciencias, esta ecuación es una mejor forma de expresar la segunda ley de Newton.
Si la fuerza neta es cero (F = 0), la ecuación anterior se convierte en:
(0 / m ) t = V - Vo
Simplificando:
0 = V - Vo
Vo = V
Es decir, al ser la fuerza neta cero sobre un cuerpo, la velocidad final de éste será igual a su velocidad inicial. Esto, en esencia, corresponde a la primera ley de Newton: un cuerpo en movimiento a velocidad constante continuará en movimiento con la misma velocidad mientras no actúe ninguna fuerza sobre él.
La primera ley de Newton también establece que un cuerpo permanecerá en reposo, mientras no actúe ninguna fuerza sobre él. Lo cual es un caso particular cuando
V = Vo = 0 m/s
Es decir, que un cuerpo inicialmente en reposo, permanecerá en reposo ( V = Vo = 0 ) mientras que la fuerza neta sobre él sea cero. De acuerdo con esto, la primera ley de Newton es consistente con la segunda ley de Newton.
This chapter will show the consistency between the first and second newton's law of motion. We will start with the mathematical expression of Newton's second law:
F = (m) (a)
If the force is constant, the acceleration it causes is also constant, which can be obtained by:
a = V - Vo / t
Combining the last two equations, we obtain:
F = m (V - Vo / t)
Reordering this equation we have:
( F/ m ) t = V - Vo
For some science teachers, this equation is a better way to express Newton's second law.
If the net force is zero (F = 0), the above equation becomes:
(0 / m ) t = V - Vo
Simplifying:
0 = V - Vo
Vo = V
*Esquembre et al. (2004) expresaron lo siguiente:
Esquembre et al. (2004) expressed the following:
Para describir un movimiento hemos previamente que precisar en qué marco de referencia (o inercial) hacemos dicha descripción. Esto nos lo da la Primera Ley de Newton que nos establece los denominados Marcos de Referencia Inerciales, aquéllos en los que son válidos las leyes del movimiento, como los referenciales en que un cuerpo que no sufre interacción alguna (o todas las interacciones a que pueda estar sometido se cancelan) se mueve con velocidad constante.
To describe a movement we must first specify in which frame of reference (or inertial) we make that description. This is given to us by Newton's First Law that establishes the so-called Inertial Frames of Reference, those in which the laws of motion are valid, such as the referential ones in which a body that does not undergo any interaction (or all the interactions to which it may be subjected are canceled) moves with constant speed.
*La primera Ley de Newton tiene interdependencia de las otras dos: sirve para establecer si un marco referencial es inercial o no lo es. Una vez establecido que un marco referencial es inercial, entonces podemos aplicar con total garantía la Segunda Ley de Newton.
Newton's first Law has interdependence from the other two: it serves to establish whether a frame of reference is inertial or not. Once it is established that a frame of reference is inertial, then we can safely apply Newton's Second Law.
*A primera vista parece como si la Primera Ley de Newton estuviera contenida en la Segunda Ley de Newton. Pero esto no es cierto. La primera Ley establece que, si sobre un cuerpo no actúa una fuerza neta, el cuerpo no estará acelerado. Esto no dice nada sobre la velocidad absoluta del cuerpo sino más bien que la velocidad del objeto no puede cambiar (aceleración) a menos que actúe una fuerza (neta) no equilibrada.
On first glance it may seem like Newton's first law is contained within Newton's second law. But this is not true. The first Law states that, if a net force does not act on a body, the body will not be accelerated. This says nothing about the absolute velocity of the body but rather that the velocity of the object cannot change (acceleration) unless an unbalanced (net) force acts.
*Pero la diferencia la marca el que la primera ley está vinculada con marcos de referencia. La primera ley es también una proposición sobre los marcos de referencia. Y ésta es la información NO contenida en la Segunda Ley. Algunas veces a la Primera Ley se la denomina Ley de la Inercia. De hecho, define un conjunto de marcos de referencia en los que la Primera Ley se cumple y que, por ello son denominados marcos inerciales de referencia.
But the difference is that the first law is linked to frames of reference. The first law is also a statement regarding reference frames. This is the information NOT contained in the second law. Sometimes the first law is also called the law of inertia. In fact, it defines a certain set of reference frames in which the first law holds, and these reference frames are therefore called inertial frames of reference.
*Puesto de otra forma, la Primera Ley de Newton establece que, si la fuerza neta actuante sobre un cuerpo es cero, es posible encontrar un (conjunto) marco de referencia en el cual el objeto está sin aceleración. Hay muchos marcos en los que el objeto se mueve con una velocidad constante.
Put another way, Newton's first law states that if the net force on an object is zero, it is possible to find at least one reference frame in which that object is stationary. There are many frames in which the object is moving with a constant velocity.
*McKelvey; Grotch (1980) manifestaron que debe notarse que la Segunda Ley de Newton contiene la información crucial de cómo se mueven los objetos cuando se les somete a la acción de las fuerzas. Por tanto, en cierto sentido la Segunda Ley de Newton ocupa una posición de importancia especial, en tanto que la primera y tercera sirven en cierta medida para ampliar la segunda. Por ejemplo, si la resultante de todas las fuerzas que actúan en un cuerpo vale cero, entonces, según la Segunda Ley, su aceleración también debe ser cero, lo que significa que está en reposo, o, a lo más, que se mueve con una velocidad que no cambia de magnitud ni de dirección. Pero esto es precisamente lo que dice la Primera Ley, de manera que se puede considerar a ésta como un caso especial de la Segunda Ley. Sin embargo, ya que es difícil describir el movimiento de objetos por influencia de fuerzas externas netas sin comprender cómo se comportan en su ausencia, y puesto que son muy comunes los casos en que es nula la resultante de todas las fuerzas en un cuerpo, generalmente se expresa la Primera Ley por separado, aunque se deduce directamente de la Segunda Ley. La Tercera Ley de Newton también apoya a la Segunda Ley, ya que dice cómo los cuerpos ejercen fuerzas entre sí, y permite distinguir las fuerzas ejercidas sobre un objeto por medios externos, de las fuerzas que ejerce éste sobre otros cuerpos.
McKelvey; Grotch (1980) stated that it should be noted that Newton's Second Law contains the crucial information of how objects move when subjected to the action of forces. In a sense, therefore, Newton's Second Law occupies a position of special importance, while the first and third serve to some extent to extend the second. For example, if the result of all the forces acting on a body is worth zero, then, according to the Second Law, its acceleration must also be zero, which means that it is at rest, or, at most, that it moves with a speed that does not change in magnitude or direction. But this is precisely what the First Law says, so it can be considered a special case of the Second Law. However, since it is difficult to describe the motion of objects by influence of net external forces without understanding how they behave in their absence, and since it is very common cases where the resulting of all forces in a body is null, the First Law is generally expressed separately, although it is deduced directly from the Second Law. Newton's Third Law also supports the Second Law, as it says how bodies exert forces on each other, and makes it possible to distinguish the forces exerted on an object by external means, from the forces exerted by it on other bodies.
-----------------------------------------------------------------------------------------------
*Si no tiene tiempo de leerlos ahora, descárguelos, imprímalos y hágalo cuando le interese (archivos en formato PDF).
If you don't have time to read them now, download, print off and take away with you (archives in PDF format).
CAPÍTULO VI: "¿POR QUÉ LA SEGUNDA LEY DEL MOVIMIENTO DE NEWTON NO ES F = (m) (a)?"
CHAPTER VI: "WHY NEWTON’S SECOND LAW OF MOTION IS NOT F = (m) (a) ?"
CHAPITRE VI : "POURQUOI LA DEUXIÈME LOI DU MOUVEMENT DE NEWTON N’EST PAS F = (m) (a) ? "
*CAPÍTULO OPTATIVO / OPTATIVE CHAPTER /CHAPITRE OPTATIF
*Sitko (2019) expresó lo siguiente:
La segunda ley enunciada por Isaac Newton en los Principia no es equivalente a F = (m) (a), como se la conoce popularmente. Este último fue descrito por Leonhard Euler, en 1752. Sin embargo, para algunos historiadores, esta formulación estaría implícita en la proposición propuesta por Newton, y de esta manera, F = (m) (a) es considerada por algunos de ellos sólo como una reformulación matemática de la ley de Newton. En este blog, inicialmente, se utilizan las consideraciones de estos historiadores y se realiza una interpretación con el fin de establecer una conexión entre la ley propuesta por Newton y F = (m) (a), utilizando el lenguaje matemático actual. A partir de esta interpretación y de una investigación bibliográfica, realizada a partir de fuentes históricas primarias y secundarias, se discuten las razones de la no equivalencia de estas leyes, así como los aspectos que conducen a esta confusión de interpretaciones; también se discuten las limitaciones de la mecánica newtoniana, que son sobre el método matemático, las coordenadas naturales y las concepciones de fuerza de Newton. A continuación, se indican los elementos no cubiertos por la mecánica de Newton, mostrando así que, de hecho, F = (m) (a) es una ley mucho más general que la propuesta por Newton.
Sitko (2019) expressed the following:
The second law enunciated by Isaac Newton in the Principia is not equivalent to F = (m) (a), as it is popularly known. The latter was described by Leonhard Euler, in 1752. However, for some historians, this formulation would be implicit in the statement proposed by Newton, and in this way, F = (m) (a) is considered by some of them only as a mathematical reformulation of Newton’s law. In this blog, initially, the considerations of these historians are used and is it is performed an interpretation in order to establish a connection between the law proposed by Newton and F = (m) (a), using current mathematical language. Based on this interpretation and on a bibliographic research, made from primary and secondary historical sources, reasons for the non-equivalence of these laws are discussed, as well as aspects that lead to this confusion of interpretations; limitations of Newtonian mechanics are discussed too, which are about mathematical method, natural coordinates, and Newton’s conceptions of force. Next, the elements not covered by Newton’s mechanics are indicated, thus showing that, in fact, F = (m) (a) is a much more general law than that proposed by Newton.
*Sitko utilizó el episodio de la construcción histórica de la Segunda Ley del Movimiento y siete puntos de vista distorsionados sobre el tema. Sitko (2020) expresó lo siguiente:
"En general, los profesores y los estudiantes tienen puntos de vista distorsionados sobre el funcionamiento de un trabajo científico. "
Sitko used the episode of the historical construction of the Second Law of Movement and seven distorted views on the subject. Sitko (2020) expressed the following:
"In general, teachers and students have distorted views on the functioning of a scientific work."
INTRODUCCIÓN
INTRODUCTION
*Es importante resaltar que Gómez, Marquina, Marquina (1984) expresaron que las dos primeras leyes de Newton tienen una enorme importancia en el sentido de que establecen las interrelaciones cuantitativas entre espacio, tiempo, materia y movimiento, y ambas constituyen el escenario y los actores del teatro del mundo real. Plantear que la primera ley es un caso particular de la segunda es un grave error conceptual.
It is important to note that Gómez, Marquina, Marquina (1984) expressed that Newton's first two laws have an enormous importance in the sense that they establish the quantitative interrelations between space, time, matter and movement, and both constitute the stage and actors of real-world theater. To state that the first law is a particular case of the second is a serious misconception.
*Asimismo, expresaron que es muy importante presentar el desarrollo de las leyes de Newton en su contexto histórico pues se trata de un bello ejemplo de la génesis de ideas científicas.
They also expressed that it is very important to present the development of Newton's laws in their historical context because it is a beautiful example of the genesis of scientific ideas.
+Asimismo, es importante considerar las ideas de Sebastiá (2013). Este investigador hace hincapié en que las Leyes de Newton no son demostrables (stricto sensu , es decir , en sentido estricto) experimentalmente.
INTENTANDO ESTABLECER UNA CONEXIÓN ENTRE LAS LEYES DE NEWTON Y F = (m) (a)
TRYING TO ESTABLISH A CONNECTION BETWEEN NEWTON’S LAW AND F= (m) (a)
*El hecho es que el principio fundamental de la mecánica apareció en 1752, escrito por Euler. Como señala Truesdell (1968), nadie duda de la ley propuesta por Newton, de su veracidad, pero lo que nadie se había dado cuenta antes de que Euler propuso el principio, es que el último era un principio general sobre los demás, que podía aplicarse a cada parte de cada sistema.
The fact is that the fundamental principle of mechanics appeared in 1752, written by Euler. As Truesdell points out (1968), no one doubts about the law proposed by Newton, of its truthfulness, but what no one had realized before Euler have proposed the principle, is that the last one was a general principle over others, which could be applied to every part of each system.
*Euler, en su Discovery of a New Principle of Mechanics (1750), propuso por primera vez la expresión de la fuerza como producto de la masa por la aceleración.
Euler, in his Discovery of a New Principle of Mechanics (1750), first proposed the expression of force as a product of mass by acceleration.
MÉTODO GEOMÉTRICO Y SUS LIMITACIONES
GEOMETRIC METHOD AND ITS LIMITATIONS
*Para Newton, los movimientos son efectos de fuerzas (o inercia), y así, él llama al estudio de la dinámica. Las fuerzas y las velocidades ya no se entienden como cualidades de los movimientos, sino como objetos matemáticos, y por lo tanto, el movimiento ya no se ve como un fenómeno externo.
For Newton, movements are effects of forces (or inertia), and so, he calls the study of dynamics. Forces and velocities are no longer understood as qualities of movements, but as mathematical objects, and thus, movement is no longer seen as an external phenomenon.
*Su método le permitió extender las matemáticas al tratamiento del movimiento de los cuerpos naturales a partir de axiomas y definiciones que dictaban cómo se producen los movimientos debido a las fuerzas. De esta manera, la mecánica newtoniana se convierte en una ciencia de los objetos matemáticos, es decir, el resultado de un proceso de matematización (Panza, 2002).
His method allowed him to extend mathematics to the treatment of the movement of natural bodies from axioms and definitions that dictated how movements occur due to forces. In this way, Newtonian mechanics becomes a science of mathematical objects, that is, the result of a process of mathematization (Panza, 2002).
*Sin embargo, el enfoque geométrico no fue suficiente para resolver problemas mecánicos más complejos. Por ejemplo, no se pudieron resolver problemas en los que se debía tener en cuenta la extensión de cuerpos, es decir, cuerpos rígidos, mucho menos los cuerpos fluidos y deformables; los problemas más complejos trajeron resoluciones muy grandes, siempre utilizando segmentos. Así, la mecánica newtoniana se limitaba a los cuerpos puntuales. Según Panza, uno de los objetivos de la mecánica analítica del siglo XVIII era hacer de esta ciencia de la geometrización del movimiento una ciencia de un objeto analítico, para que estas resoluciones pudieran abarcar una clase más general de problemas, y de forma más práctica y sistemática.
However, the geometric approach was not enough to solve more complex mechanical problems. For example, problems in which the extension of bodies should be taken into account, that is, rigid bodies, could not be solved, much less the fluid and deformable bodies; more complex problems brought very large resolutions, always using segments. Thus, Newtonian mechanics was limited to punctual bodies. According to Panza, one of the aims of analytical mechanics of the eighteenth century was to make this science of geometrization of motion a science of an analytical object, so that these resolutions could cover a more general class of problems, and more practically and systematically.
USO DE COORDENADAS NATURALES
USE OF NATURAL COORDINATES
*Los problemas en aquel momento fueron tratados con los coordenadas naturales supuestos. Para utilizar estos, en cada punto de la trayectoria, fue necesario establecer dos marcos de referencia "naturalmente" elegidos por las curvas tangentes y normales de la situación, de acuerdo con el contexto del problema (Stan, 2017). Según este uso, era necesario tener una cierta capacidad para percibir cuál era el referencial más natural, y este método no era aplicable a cuerpos extensos ni a movimientos tridimensionales. De este modo, no se cubrió una clase muy grande de problemas.
The problems at that time were treated with the so-called natural coordinates. To use these, at each point in the trajectory, it was necessary to establish two reference frames “naturally” chosen by the tangent and normal curves of the situation, according to the context of the problem (Stan, 2017). According to this use, it was necessary to have a certain ability to perceive which was the most natural referential, and this method was not applicable to extensive bodies nor three-dimensional movements. In this way, a very large class of problems was not covered.
CONCEPTOS DE FUERZA
CONCEPTS OF FORCE
* Entonces, es posible ver que estamos tratando con dos formulaciones equivalentes a lo que Newton describe en sus borradores: F = (m) (a) y F = Δ (m v). Sin embargo, la declaración de la segunda ley del movimiento, que aparece en los Principia, será equivalente a F = Δ (m v). Por otra parte, ninguna parte de su obra es F = (m) (a) o el principio conceptual que le da un significado como la ley del movimiento. Westfall (Maltese, 1992) señala esta ambigüedad en la obra de Newton, que es la causa de mucha controversia hoy en día con respecto a su conceptualización de la fuerza, y lo que conduce a la confusión sobre su enunciación de la segunda ley.
Then, it is possible to see that we are dealing with two formulations equivalent to what Newton describes in his drafts: F = (m) (a) and F = Δ (m v). However, the statement of second law of motion, which appears in the Principia, will be equivalent to F = Δ (m v). Moreover, nowhere of his work is F = (m) (a) or the conceptual principle that gives it a meaning as the law of motion. Westfall (Maltese, 1992) notes this ambiguity in Newton’s work, which is the cause of much controversy today regarding his conceptualization of force, and what leads to confusion about his enunciation of the second law.
* De la proposición de la segunda ley propuesta por Newton, si tenemos en cuenta algunos supuestos, como hicimos anteriormente, aun así, el camino hacia F = (m) (a) no es trivial, y ahora acabamos de demostrar por qué no hay consenso sobre si Newton quería decir F = (m) (a) o F = Δ (m v): sus concepciones de la fuerza eran confusas debido a la ambigüedad mantenida entre el uso de fuerzas continuas y discretas, y aún queda mucho por pensar fuera, elaborado y unificado, hasta que se pudo llegar al principio de la mecánica en el forma moderna, F = (m) (a).
From the statement of the second law proposed by Newton, if we take into account some assumptions, as we did previously, even so, the path to F = (m) (a) is not trivial, and now we have just shown why there is no consensus about whether Newton meant F = (m) (a) or F = Δ (m v) : his conceptions of force were confuse because of the ambiguity maintained between the use of continuous and discrete forces, and much still needed to be thought out, elaborated and unified, until one could arrive at the principle of mechanics in the modern form, F = (m) (a)
DEPENDENCIA ENTRE LAS LEYES
DEPENDENCE BETWEEN THE LAWS
*En la segunda ley de Newton, el movimiento de un cuerpo sería una secuencia de pequeños "accidentes cerebrovasculares", y la ley se referiría a lo que sucede cuando se aplica el accidente cerebrovascular, y la primera ley es válida cuando no hay accidente cerebrovascular. Para Newton, la primera ley sería requerida cuando se trabaja con la segunda. Hoy en día, utilizamos la primera ley para definir marcos de referencia inerciales en los que la segunda ley es válida.
In Newton’s second law, the motion of a body would be a sequence of small “strokes”, and the law would refer to what happens when the stroke is applied, and the first law is valid when there is no stroke. For Newton, the first law would be required when working with the second one. Nowadays, we use the first law to define inertial reference frames in which the second law is valid.
*El principio propuesto por Euler expresa la segunda ley de Newton relacionada con un sistema de marco de referencia independiente, en coordenadas cartesianas ortogonales. No solo eso, sino que si la fuerza resultante sobre el cuerpo es nula, se observa que su velocidad se vuelve constante, es decir, si no actúa ninguna fuerza, el movimiento es rectilíneo uniforme, de acuerdo con la primera ley de Newton. De la segunda ley escrita por Newton, no se puede deducir (Maronne & Panza, 2014): con ella, sabemos que si la fuerza es cero, el movimiento no se altera. Sin embargo, no se puede decir que haya un movimiento rectilíneo uniforme. Para ello, sería necesario basarse concomitantemente en la primera ley, que establece que el cuerpo permanece en su estado de movimiento, si ninguna fuerza actúa sobre él, o si el resultado de las fuerzas que actúan sobre él es cero.
The principle proposed by Euler expresses Newton’s second law related to an independent reference frame system, in orthogonal Cartesian coordinates. Not only that, but if the resultant force on the body is null, it is noted that its velocity becomes constant, that is, if no force acts, the motion is uniform rectilinear, agreeing with Newton’s first law. From the second law written by Newton, one cannot deduce it (Maronne & Panza, 2014): with it, we know that if the force is zero, the motion is not altered. However, it cannot be said that there is a uniform rectilinear motion. For this, it would be necessary to rely on the first law concomitantly, which states that the body remains in its state of motion, if no force acts on it, or if the resultant of the forces acting on it is zero.
*Así, se percibe que existe una dependencia entre las leyes propuestas por Newton. Estas elaboraciones y las de Euler son entonces sustancialmente diferentes (*), es decir, ha habido una evolución conceptual entre las dos formas de escritura (no solo de escritura sino de significado) la ley del movimiento (Maltese, 1992), así como también con la primera ley: la inercia ya no es la causa de la primera ley, sino que ofrece una definición de marco de referencia inercial (**)
Thus, it is perceived that there is a dependence between the laws proposed by Newton. These and Euler’s elaborations are then substantially different (*), that is, there has been a conceptual evolution between the two forms of writing (not only of writing but of meaning) the law of movement (Maltese, 1992), as well as also with the first law: inertia is no longer the cause of the first law, but it offers a definition of inertial reference frame (**)
(*)La segunda ley puede ser vista como el resultado de una serie de experimentos y observaciones, que es la llamada visión sintética, defendida por Newton, o puede ser vista como una definición, una función, que es la proposición analítica funcional defendida por Euler (Buchdahl, 1951).
The second law can be seen as the result of a series of experiments and observations, which is the so-called synthetic view, defended by Newton, or can be seen as a definition, a function, which is the functional analytic proposition defended by Euler (Buchdahl, 1951).
(**)El nuevo principio, de alguna manera, modifica el significado de la primera ley. Inicialmente para Newton, se necesitaba una causa para hacer que el movimiento perseverara. Sus estudios sobre Descartes le hicieron cambiar su concepción, pero la idea de la inercia como fuerza interna al cuerpo permanece en toda su obra (Chang, 2014).
The new principle, somehow, modifies the meaning of the first law. Initially for Newton, one cause was needed to make the movement persevere. His studies about Descartes made him change his conception, but the idea of inertia as an internal force to the body remains in all his work (Chang, 2014).
CASO ANGULAR
ANGULAR CASE
*En la enunciación de Newton de la segunda ley, afirma que la variación del movimiento ocurre en la dirección de la acción de la fuerza. Sin embargo, esto no es válido para otros tipos de problemas, como los casos de rotación, donde es necesaria la introducción de un concepto de movimiento adecuado al movimiento de rotación. Más tarde, Euler se da cuenta de que se necesitan nuevos principios para resolver, junto con este caso, una clase más grande de problemas.
In Newton’s enunciation of the second law, he states that the variation of motion occurs in the direction of the force’s action. However, this is not valid for other types of problems, such as the rotation cases, where is needed the introduction of a concept of motion appropriate to the rotation movement. Later, Euler realizes that new principles are then needed to solve, along with this case, a larger class of problems.
¿QUÉ NO HIZO NEWTON?
WHAT NEWTON DIDN’T DO?
*Por otro lado, no se puede dejar de mencionar que Newton organizó y dedujo leyes y fenómenos aparentemente independientes entre sí, creó nuevos conceptos, comparó sus predicciones con valores medidos, trajo conceptos dinámicos genuinos, y ya no los derivados de la estática, como se hizo una vez. Sin embargo, no podía ofrecer la forma clásica que usamos hoy en día de la mecánica ya que sus principios no eran claros y precisos (Truesdell, 1975). Por lo tanto, Newton puede ser considerado como el que inició los preparativos para la formulación de , pero dicha formulación tuvo innumerables sucesores para la "producción de mecánica".
On the other hand, one cannot fail to mention that Newton organized and deduced laws and phenomena seemingly independent of each other, created new concepts, compared his predictions to measured values, brought genuine dynamic concepts, and no longer those derived from static, as was once done. However, he could not offer the classical form we use today of mechanics since his principles were not clear and precise (Truesdell, 1975). Thus, Newton can be considered as the one who initiated the preparations for the formulation of , but such formulation had countless successors for the “production of mechanics”.
*Como vimos anteriormente, existe una incompatibilidad entre la afirmación propuesta por Newton y lo que conocemos por la segunda ley de Newton, a saber, F = (m) (a). Efectivamente, al hacer un análisis documental, podemos ver que ni ninguna otra ecuación diferencial están incluidas en los Principia. En los años siguientes, le valió a otros estudiosos buscar principios que mostraran estas ecuaciones para los sistemas de Newton y para los problemas que otros científicos aún estarían estudiando. Nombres como Euler han perfeccionado los desarrollos newtonianos, creando nuevos campos, conceptos, formalismos, etc., incluso porque, en el siglo XVIII, los Principia no eran el único trabajo de mecánica: todavía estaban los lados de Huygens y Leibniz (que tenían seguidores como Hermann y los Bernoullis) (Stan, 2017), Varignon y la tradición de conceptos y métodos estáticos, newtonianos, el estudio de la relación entre fuerzas y sus deformaciones de Johann Bernoulli, y finalmente, Euler y la unión entre los conceptos newtonianos y el formalismo de Leibniz. Esta narración se extiende hasta 1788, con la obra de Lagrange, Mécanique Analytique, que finaliza los desarrollos de la hoy llamada Mecánica Clásica.
As we saw earlier, there is an incompatibility between the statement proposed by Newton and what we know by Newton’s second law, namely, F = (m) (a). Effectively, by doing a documentary analysis, we can see that neither nor any other differential equation are included in the Principia. In the following years, it was up to other scholars to seek principles that would show these equations for Newton’s systems and for problems that other scientists would still be studying. Names such as Euler have perfected the Newtonian developments, creating new fields, concepts, formalisms, etc., even because, in the eighteenth century, the Principia were not the only work of mechanics: there were still the Huygens and Leibniz sides (that had followers like Hermann and the Bernoullis) (Stan, 2017), Varignon and the tradition of static, Newtonian concepts and methods, the study of the relation between forces and its deformations of Johann Bernoulli, and finally, Euler and the joint between Newtonian concepts and the formalism of Leibniz. This narrative extends to 1788, with the work of Lagrange, Mécanique Analytique, which finalizes the developments of the today called Classical Mechanics.
LA ENSEÑANZA DE LAS CIENCIAS Y LA SEGUNDA LEY
SCIENCE TEACHING AND THE SECOND LAW
*En el episodio de la segunda ley, como hemos visto anteriormente, ciertos conceptos y formalismos definidos después de Newton se presentan como la creación de él, omitiéndose las contribuciones de otros científicos para esa cuestión. Este tipo de omisión histórica puede conducir a una imagen distorsionada de cómo se construye la Ciencia, llevando la imagen de mentes brillantes aisladas productores de conocimiento, e ignorando el papel del trabajo colectivo y cooperativo. No sólo en lo que respecta al proceso histórico, sino que esta omisión, como hemos visto, puede dificultar la comprensión de ese concepto físico, mientras que dice que el enunciado hecho por Newton corresponde a la ecuación propuesta por Euler.
In the episode of the second law, as we have seen previously, certain concepts and formalisms defined after Newton are presented as the creation of him, being omitted the contributions of other scientists for that question. This kind of historical omission can lead to a distorted image of how Science is constructed, bringing the image of isolated brilliant minds productors of knowledge, and ignoring the role of collective and cooperative work. Not only concerning the historical process but this omission, as we have seen, can difficult the understanding of that physical concept, while it says that the enunciate made by Newton corresponds to the equation proposed by Euler.
* Además, la redacción de la Segunda Ley, tal como se presenta en los Principia, y que es prácticamente el mismo que el que se presenta en los libros de texto, seguido de la formulación F = (m) (a), no proporciona una relación directa, y, para el estudiante ser capaz de comprender la relación entre la redacción original y la fórmula Euleriana, el enfoque histórico es necesario.
Moreover, the wording of the Second Law, as presented in the Principia, and which is practically the same as the one presented in textbooks, followed by the formulation F = (m) (a), does not provide a direct relationship, and, for the student to be able to understand the relationship between the original wording and the Eulerian formula, the historical approach is necessary.
*Por lo tanto, se argumenta que el uso del enfoque histórico es beneficioso para la enseñanza, y con este trabajo, se espera que la idea de la Ciencia como un proceso de construcción a lo largo del tiempo y por diferentes científicos esté mejor establecida.
Therefore, it is argued that the use of historical approach is beneficial to teaching, and with this paper, it is expected that the idea of Science as a process of construction over time and by different scientists be better established.
-------------------------------------------------------------------------------------------
*Si no tiene tiempo de leerlos ahora, descárguelos, imprímalos y hágalo cuando le interese (archivos en formato PDF).
If you don't have time to read them now, download, print off and take away with you (archives in PDF format).